抽样sampling
从事物总体中随机或有代表性地抽取样本的方法。运用数理统计方法通过抽样样本的统计量,可对总体参数作出统计推断。在农业机械试验鉴定中,一般用抽样调查方法获取各种试验和调查的观测值;用抽样检查方案确定农业机械或部件的质量水平。
样本 是取自总体中的一个或多个个体,用于提供有关总体的信息,作为可能作出对总体的某种判定的基础。总体是所考虑的个体的全体,个体是一个自然单位或若干自然单位的组合,可用一个定性或定量的观测值(即一次观测或试验所确定的特性值)代表。取自总体的一个个体或在多级抽样中的一组个体称为抽样单位。样本中所包含的抽样单位数称为样本大小,以n表示。样本大小与抽取此样本的总体(或子总体)的大小之比称为抽样比。从样本中再抽取样本称为子样本。
确定样本大小 在抽样检查产品时,由抽取的样本大小n对整批产品作出“接收”或“拒收”的判断,可能出现两类错误:第Ⅰ类错误或称生产方风险,是把可接收的整批产品错判为不合格而加以“拒收”;第Ⅱ类错误或称使用方风险,是把质量不合要求的整批产品错判为合格而加以“接收”。样本大小n的确定,应使犯第Ⅰ类和第Ⅱ类错误的概率都不大于预先给定的概率α和β。常用的概率是0.10,0.05或0.01。此外,总体算术平均值为μ0或不合格品率为P0的分布总体方差σ20,以及允许的临界值为μ1或P1的分布的总体方差σ21,采用单侧检验或双侧检验等方面来确定。若改变任何一方面条件或样本大小,都会引起相应的变动,因此,对确定样本大小要权衡得失,统一平衡,寻求适宜而经济(检查费用和由于犯第Ⅰ、Ⅱ类错误所引起的损失大小等)的抽样方案,它可以用统计计算、检查特性曲线或查表等方法来确定。
统计推断 在确定样本大小后,就可以确定置信区间和单侧检验置信限T,双侧检验置信限T1和T2来进行假设检验。如果只是为了显著性检验,当在所确定的样本大小下所得的统计量的算术平均X或不合格品率p1落入拒绝域,则拒绝原假设H0而不拒绝备择假设H1,否则就不拒绝原假设H0而拒绝备择假设H1。如果不但要作显著性检验,而又要知道它们之间的差异有多大,则把假设检验转换为订出一个合格判定数(值)以判断拒绝或不拒绝假设,这在抽样检查中,由于着重在产品或部件的质量水平检查,通常是采用的。对连续随机变量,设原假设H0(μ≤μ0)及H1(μ>μ0),计算置信限T作为合格判定值,或以μc表示。抽样方案订为(N,n,μc),当统计量的算术平均X小于判定值μc时,就判为合格,不拒绝原假设,否则为不合格而拒绝原假设。对离散随机变量,若原假设H0(P≤P0)及H1(P>P0),计算置信限T后,乘以样本大小n得合格判定数c,抽样方案为(N,n,c),当样本不合格品数d小于c时,则判为合格,不拒绝原假设,否则判为不合格而拒绝原假设。
抽样调查方法
简单随机抽样 从包含N个总体单位的总体中,抽取n个总体单位作为样本单位,使包含有n个样本单位的样本中的所有可能的组合被抽取的概率相等。
系统抽样 将一个总体中的N个子总体单位系统排列(例如按生产顺序),并从1到N编号。随机选一正整数k,再从1到k中随机抽取h,系统抽样是抽取编号h,h+k,h+2k,……,h+(n-1)k的n个总体单位作为样本单位,抽样调查中常用的等距离、等间隔抽样,如棋盘式、对角式等都属于系统抽样。系统抽样比较简单,但是按顺序的等间距出现周期性变异时,所抽取的样本表现有偏性而难以估计点值,而且前后观察值间会出现自相关现象。系统抽样除了h编号是随机抽取外,其他都是顺序、等间距抽取的,它不属随机抽样。为解决试验误差的计算问题,可采用系统抽样与多级抽样或整群抽样相结合的方法。
多级抽样 一种分级抽样的方式,第一级抽样是先按规定的若干抽样单位,从总体中随机抽取样本。然后按规定的级数,逐级从上一级样本中随机抽取子样本,每一级抽样单位比上一级的少。当以少量的样本单位或子样本单位来进行分析研究时,以采用多级抽样较为适宜。
分层抽样 根据总体的变异情况,将总体分为若干较均匀、同质的子总体(或称层、区)。独立地从每层、区中相等地或按层、区大小比例随机抽取所需子样本单位数。分层抽样可以克服简单随机抽样和系统抽样的缺点。如总体的主要变异是明显的由子总体(层、区)之间的变异形成的,则采用分层抽样较为适宜。
整群抽样 将总体分为许多群(区),随机地抽取若干群,并由这些群中所有子样本单位组成子样本。当总体的主要变异来自群内各子样本单位之间或小范围的群间,则以采用整群抽样较为适宜。
双重抽样 当所研究调查的性状特征的观测值难于直接测定时,可以间接测定另一种易于测定而与前一种存在相关关系的性状特征,利用回归方程估计前一种性状特征的观测值。
抽样检查方案 为了决定样本大小和判断产品的检查批的质量是否合格而规定的一组检查方案。根据生产情况,凡产品已经构成成批的检查,称为逐批检查;凡产品不能构成成批检查的,称为连续检查。
单式与复式抽样 单式抽样的一次抽样方案是从批中只抽取一个样本来判断合格或不合格。复式的多次抽样方案是根据第一次样本的检查结果来判断合格和不合格或再作检查,如果再作检查则根据第一次样本分别与随后样本的逐个检查结果来判断合格与不合格。随后样本的检查次数是事先规定的。在复式二次抽样后再作多次抽样时,一般抽到3~5个样本。
序贯抽样 逐个(或成组)地抽取个体,但事先并不固定抽取的个数。根据事先规定的规则,抽到可以作出拒绝或接受此批的决定为止。
调整型抽样 检查一批批产品的质量是否产生变化。当产品质量正常时用正常抽样检查方案;当产品质量发生变化(提高或变劣)时,可以相应采用放宽、特宽或加严的检查方案来调查抽样检查方案。
标准型抽样 对孤立的一批产品,标准型抽样方案不需要利用产品质量的历史资料,同时能控制第Ⅰ、Ⅱ类错误的概率,但需要较多的产品单位来进行检查。
挑选型抽样 对不合格品进行百分之百的检查,以合格件替代后再进行检查,虽然它是利用以往资料,但不调整抽样检查方案。
链式抽样 在因条件限制或破坏性的检查而只能抽取很小的样本,且在样本中不允许有不合格品时,即以合格判断给定数c=0的抽样检查方案,把一批批产品的样本看作相应的链式环节,一批产品是否合格涉及到链式的每个环节。在前几批样本中如未出现不合格品,即使在这批中出现一个不合格品,仍不拒绝这批产品。如在前几批中曾出现过不合格品,就拒绝这批产品。在链式抽样方案中,通常取3、4或5批产品,可根据情况而定。
抽样sampling
根据对总体部分样本的调查结果,来估算总体的方法。具相同性质的一群事物叫总体,总体是有限的且肯定存在的,并具有一定容量或数量。如稻田纵卷叶螟和褐飞虱各为一个总体。总体的数量过大时,一一数清必然困难,通常采用抽样的方法,通过样本的计算,可以获得总体的资料。抽样是以总体的分布规律和大数定律为依据的。按其分布型选用适当的抽样方式,从总体随机选取一部分抽样单位,已确定的抽样单位需全部调查,且不能用别的单位代替。大数定律是:具有小概率的事件出现可能性是很小的,有时可以忽略不计;若某一事件的概率很大,则出现可能性大,大数定律就是要找出概率接近1的规律,以随意接近于1的概率来估算某事件的发生。抽样调查所获的平均数是估计值,从样本所得的估计值与总体的绝对值或真值的差异,称抽样误差,一般是用样本平均数标准差(S)表示。昆虫学调查中,抽样用于种群密度调查、自然种群生命表研究、害虫为害程度调查、害虫预测预报和害虫防治效果调查等方面。
抽样方法 按组织的方式,抽样方法可分:随机抽样,分层抽样、多级抽样,序贯抽样和系统抽样等。一般常用的抽样方法,可分别采取以下方法抽取抽样单位(见图):❶五点抽样:适于密集的或成行的植物及随机分布型的昆虫调查,可按面积、长度或植株数作抽样单位;
❷对角线抽样:适于密集的或成行的植物及随机分布型昆虫。又分单对角线和双对角线两种;
❸棋盘式抽样;适于密集的或成行的植物及随机分布型或聚集分布型的昆虫;
❹平行线抽样:也称分行式抽样,适于成行的植物及聚集分布型的昆虫;
❺Z形抽样:适于嵌纹分布型的昆虫。
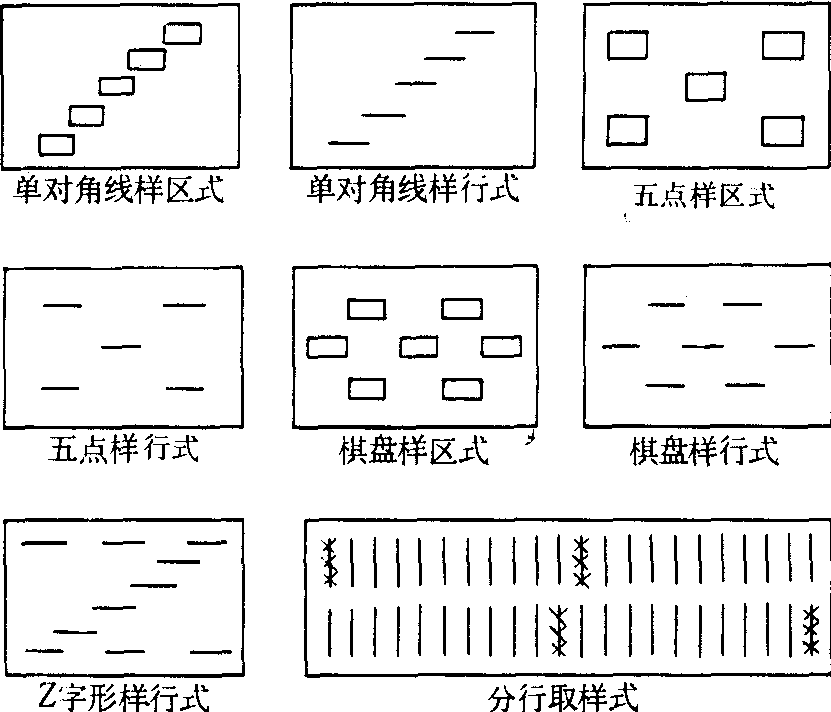
几种常用的抽样方法
抽样单位 见抽样单位。
样本数量 调查的抽样方法和抽样单位决定以后,就要决定抽样数量。如果抽样过多,就需花费较多时间和人力,抽样太少又影响估计量准确性。故确定适当抽样数至为重要。可根据害虫分布型和采取的抽样方法决定抽样数量。
❶总体呈负二项式分布时,有放回抽样 (重复抽
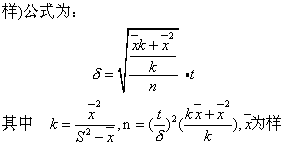
本平均数,S2 为样本方差,n为抽样数,δ为允许误差。
无放回抽样(不重复抽样)公式为:
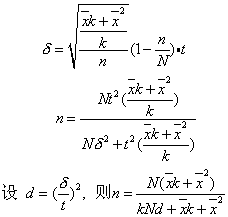
式中 N为总体数。
❷总体呈泊松分布时,有放回抽样公式为:
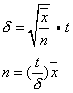
无放回抽样公式为:
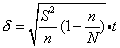
因S2=(泊松分布的特点), 则
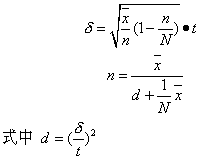
抽样Chouyang
统计学研究的一种基本方法,指从事件的总体中抽出一部分(即样本)作为研究的对象。在心理学研究中,可以针对行为或心理特质总体进行抽样,也可以针对被试的总体进行抽样。所抽取的样本要具有代表性,能反映总体的特征。抽样的方法主要有随机抽样和分层抽样两种。当总体同质性较高时,采用随机抽样,随机地抽取其中一部分作为样本;如果总体中包含几类个体,采用分层抽样,即按比例从这几类中各自随机地取出一些个体放在一起组成一个样本。样本中所含个体的数目称为样本容量。样本容量太小会产生较大的随机误差,使样本值与总体值相差太大;样本容量太大又会给结果的统计带来麻烦,失去抽样的意义。因此,要根据研究的目的、性质以及总体的情况适当地确定样本的容量。
抽样sampling
又称“采样”。把时间连续的模拟信号变成时间离散的样值序列的过程。通常采用时间间隔为Ts的均匀抽样脉冲序列St(t)与模拟信号f(t)的乘积来表示抽样的结果,形成包络为f(t)的脉幅调制信号fs(t)。抽样定理指出:一个最高频率为fm的限带信号f(t),可以惟一地用间隔为Ts=1/(2fm)的样值序列fs(t)来确定。若由单位冲激脉冲构成理整抽样脉冲序列dt(t)的抽样频率fs=1/Ts不小于2fm,则fs(t)的频谱Fs(w)为原来模拟信号频谱F(w)在以nws(n=0,±1,±2,…)为中心处的复现而无混叠。用截止频率为fm的低通滤波器可从fs(t)中恢复原信号。2fm通常称为奈奎斯特频率,抽样定理也称为奈奎斯特抽样定理,是数字通信的理论基础。据此进行抽样获得离散时间信号序列,为量化、编码和时分复用提供条件。