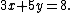“Flat (geometry)”的意思、由来-开放百科全书

词条

Flat (geometry)

释义

Descriptions
By equations Parametric
Operations and relations on flats
Intersecting, parallel, and skew flats Join Properties of operations
Euclidean geometry
See also
Notes
References
External links

linear subspace in the real n-space}} not redirected yetdimensional space, there are flats of every dimension from 0 to {{math|n − 1}}.^[1] Flats of dimension {{math|n − 1}} are called hyperplanes.

Flats are the affine subspaces of Euclidean spaces, which means that they are similar to linear subspaces, except that they need not pass through the origin. Flats occurs in linear algebra, as geometric realizations of solution sets of systems of linear equations.

A flat is manifold and an algebraic variety, and is sometimes called linear manifold or linear variety for distinguishing it from other manifolds or varieties.

Descriptions

By equations

A flat can be described by a system of linear equations. For example, a line in two-dimensional space can be described by a single linear equation involving {{mvar|x}} and {{mvar|y}}:

In three-dimensional space, a single linear equation involving {{mvar|x}}, {{mvar|y}}, and {{mvar|z}} defines a plane, while a pair of linear equations can be used to describe a line. In general, a linear equation in {{mvar|n}} variables describes a hyperplane, and a system of linear equations describes the intersection of those hyperplanes. Assuming the equations are consistent and linearly independent, a system of {{mvar|k}} equations describes a flat of dimension {{math|n − k}}.

Parametric

A flat can also be described by a system of linear parametric equations. A line can be described by equations involving one parameter:

while the description of a plane would require two parameters:

In general, a parameterization of a flat of dimension {{mvar|k}} would require parameters {{math|t₁, … , t_k}}.

Operations and relations on flats

Intersecting, parallel, and skew flats

An intersection of flats is either a flat or the empty set.^[2]

If every line from the first flat is parallel to some line from the second flat, then these flats are parallel. Two parallel flats of the same dimension either coincide or do not intersect; they can be described by two systems of linear equations which differ only in their right-hand sides.

If flats do not intersect, and no line from the first flat is parallel to a line from the second flat, then these are skew flats. It is possible only if sum of their dimensions is less than dimension of the ambient space.

Join

For two flats of dimensions {{math|k₁}} and {{math|k₂}} there exists the minimal flat which contains them, of dimension at most {{math|k₁ + k₂ + 1}}. If two flats intersect, then the dimension of the containing flat equals to {{math|k₁ + k₂}} minus the dimension of the intersection.

Properties of operations

These two operations (referred to as meet and join) make the set of all flats in the Euclidean {{mvar|n}}-space a lattice and can build systematic coordinates for flats in any dimension, leading to Grassmann coordinates or dual Grassmann coordinates. For example, a line in three-dimensional space is determined by two distinct points or by two distinct planes.

However, the lattice of all flats is not a distributive lattice.

If two lines {{math|ℓ₁}} and {{math|ℓ₂}} intersect, then {{math|ℓ₁ ∩ ℓ₂}} is a point. If {{mvar|p}} is a point not lying on the same plane, then {{math|1=(ℓ₁ ∩ ℓ₂) + p = (ℓ₁ + p) ∩ (ℓ₂ + p)}}, both representing a line. But when {{math|ℓ₁}} and {{math|ℓ₂}} are parallel, this distributivity fails, giving {{mvar|p}} on the left-hand side and a third parallel line on the right-hand side.

Euclidean geometry

The aforementioned facts do not depend on the structure being that of Euclidean space (namely, involving Euclidean distance) and are correct in any affine space. In a Euclidean space:

There is the distance between a flat and a point. (See for example Distance from a point to a plane and Distance from a point to a line.)

There is the distance between two flats, equal to 0 if they intersect. (See for example Distance between two lines (in the same plane) and Skew lines#Distance.)

There is the angle between two flats, which belongs to the interval {{closed-closed|0, π/2}} between 0 and the right angle. (See for example Dihedral angle (between two planes). See also Angles between flats.)

Notes

1. ^In addition, a whole {{mvar|n}}-dimensional space, being a subset of itself, may also be considered as an {{mvar|n}}-dimensional flat.
2. ^Can be considered as {{num|−1}}-flat.

References

Heinrich Guggenheimer (1977) Applicable Geometry,page 7, Krieger, New York.
{{citation

| last = Stolfi
| first = Jorge
| title = Oriented Projective Geometry
| publisher = Academic Press
| date = 1991
| isbn = 978-0-12-672025-9 }}
From original Stanford Ph.D. dissertation, Primitives for Computational Geometry, available as DEC SRC Research Report 36.

External links

{{MathWorld|urlname=Hyperplane|title=Hyperplane}}
{{MathWorld|urlname=Flat|title=Flat}}

Hyperplan

3 : Euclidean geometry|Affine geometry|Linear algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。