收敛数列的性质shoulian shulie de xingzhi

❶若数列 {a_n} 收敛，则它只有一个极限。

❷若数列 {a_n}收敛，则数列 { a _n}有界，即存在正数M，使得对任意自然数n有|a_n|≤M。
性质
❷的等价命题是：无界数列必发散，可利用这个命题判断某些数列的发散性。例如，对于数列{n cos nπ}，由于它无界，故发散。
有界性只是数列收敛的必要条件，而不是充分条件，例如，数列 {sin n}有界，但它并不收敛。

❸若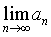＝a>0 (或<0)，则对任意一个满足不等式a>a′ >0 (或aN时，an>a′ >0 (或a n
❹若且存在自然数N，使当n>N时有a_n≤b_n，则a≤b。
若把性质
❹中的a_n≤b_n换成a_nn，结论仍为a≤b。

❺若数列 {a_n}收敛于a，则它的任何一个子数列{an_k} 也收敛于a。
性质
❺的等价命题有：若数列{a_n}的某一个子数列发散，则数列 {a_n}发散；若数列 {a_n}的两个收敛子数列不收敛于同一极限，则数列 {a_n}发散，这些命题也可用来判断一些数列的发散性，例如，对于数列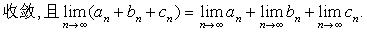它的偶数项子数列收敛于0，而另一子数列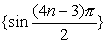收敛于1，所以数列 发散。
性质
❺的逆命题成立，即着数列 {a_n}的任何一个子数列都收敛于常数a，则数列 {a_n} 收敛于a。
上述五个性质都可利用数列极限的定义直接证明。