数乘向量shucheng xiangliang

几个相等的非零向量a相加所得的和向量，叫作正整数n与向量a的积，记为na，即

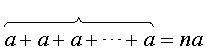
从这个狭义的定义中抽象出来，我们得到数乘向量的定义：
一个数m乘一个向量a，结果是一个向量ma，称为数乘向量的积，其模是|m||a|.当m>0时，ma与a同向，当m<0时，ma与a反向，当m=0时，0a=0.
这个定义可以形象地理解为，把向量a伸缩|m|倍，再由m的符号确定是否调向.
数乘向量有以下四条运算规律：
❶交换律 ma=am;

❷结合律 m(na)=(mn)a;

❸第一分配律 (m+n)a=ma+na;

❹第二分配律 m(a+b)=ma+mb.

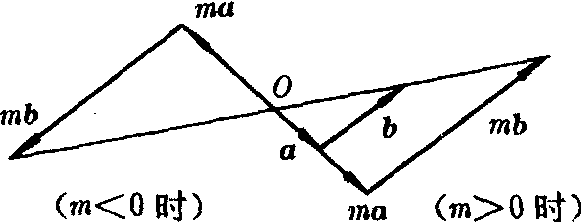
根据“方向相同，模相等”这两个向量相等的条件，很容易证明上述交换律、结合律和第一分配律.第二分配律的成立可以根据相似三角形的性质从图中得到直观的证明.