方差分析fangcha fenxi

指教育实验中分析数据的一种基本方法。进行教育实验所取得的数据都包含着两种变差：❶条件变差。是由实验处理或实验条件不同而造成的差异；
❷随机变差。是由实验处理或实验条件之外的随机因素所造成的差异。方差分析的目的就是设法把这两种变差分开，进而加以比较。如果条件变差（亦称组间变差）比随机变差（亦称组内变差）大，就说明处理或条件重要而不可忽视；如果它们之间相差较小，则说明处理或条件并不重要而可予忽略。
方差分析的基本思想是把样本中存在的总变差(以“平方和”表示)分解成处理之间（或组间）的变差和处理内部（或组内）的变差，即

然后把它们的平方和变成方差（除以各自的自由度），进而把这两种方差作比，即

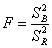
显然，这个统计值服从于F分布。
如果实验处理不发生作用，则SB2与SE2就可看成均来自同一总体的随机变差，即SB2与SB2相差不大，比值近似于1；如果实验处理发生了明显的作用，则SB2就不能看作是随机变差，而是看作来自含处理在内的更大总体的变差，这时SB2必大于SB2，比值就远大于1，即统计值F将落入F分布的右尾。因此，当计得F值落入F分布的右尾时，我们就否定处理之间没有差异的假设。
单因素的方差分析 对一种变量实施K种不同处理的结果，进行上述的方差分析，就称为单向方差分析。
当在K种实验处理之间有明显的差异时，我们还要区别造成这种差异是由于处理条件不同、还是由于某些处理的总体方差本来就较大呢？为此，对K种处理或K个样本进行方差分析时，必须假定这K个正态总体的方差相等或近似。有了这个假定，我们就可断定K种处理间的明显差异，主要是由于实施不同实验处理所致。
[例] 为鉴定4种不同数学教材的效果，分别在教师和学生水平相同的4所学校中各试行一种教材。经过一教学阶段后，从各校的试验班中随机抽取10个学生进行统测，结果如下：
教材Ⅰ:38 40 42 49 34 48 35 34 48 39教材Ⅱ:44 40 38 41 59 48 49 42 54 23教材Ⅲ:61 40 54 64 50 45 50 30 46 63教材Ⅳ:48 59 63 45 37 58 52 54 40 60问：这4种不同教材的教学效果是否有显著差异？
显然，这4种教材的平均数不同，说明存在处理或条件变差；其次同一种教材下的学生成绩也不同，说明存在随机变差。为了检验不同教材的效果，可以对每对平均数作显著性检验，但需作C42=6次的检验，这样做不但耗时费力，而且降低检验的可靠性。方差分析可以较好地解决这一问题。为此设H₀:u₁＝u₂＝u₃＝u₄。
第一步求各处理的平均数和标准差：₁＝40.7、S12=34.5、2=43.8、S22=96.8、3=50.3、S32=115.8、₄＝51.6、S42=78.5(总平均数r=46.6)。
第二步依下式求处理之间（或组间）的方差：

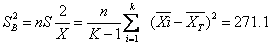
第三步依下式求处理之内（或组内）的方差：

第四步计统计值：

第五步作显著性检验。据f₁＝k-1=3,f₂＝k(n-1)=36及a=0.05，在F分布表中可查到F(_3,36)0.95＝2.872。因F>F(_3,36)₀.₉₅，故拒绝H₀，即认为不同教材的效果是明显不同的。
兹把上述单因素（教材）方差分析的一般形式概括如下(见表1与表2)。

容量相同的单因素方差分析表

表1 (H₀:u1=u2=…=uK)

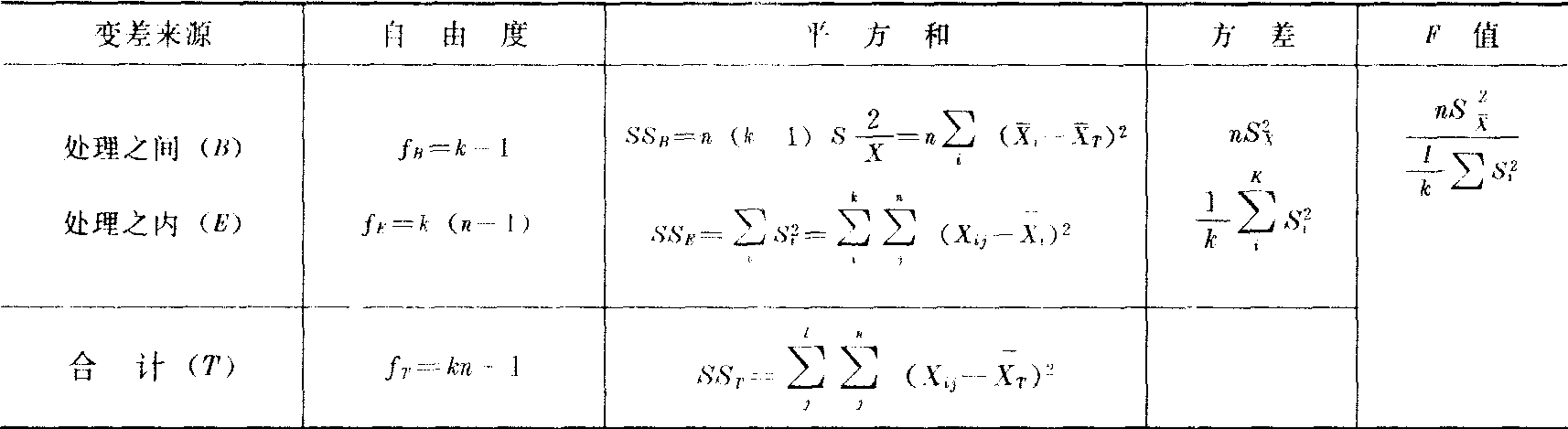
在上例中据表1的方差分析表为：

变差来源	自由度	平方和	方差	F值
教材之间 教材之内	3 36	813.3 2930.4	271.1 81.4	3.33*
合 计	39	3743.7

当容量不同时，则表1变为表2:

容量不同的单因素方差分析表

表2 (H₀:u₁＝u₂＝…=u_k)

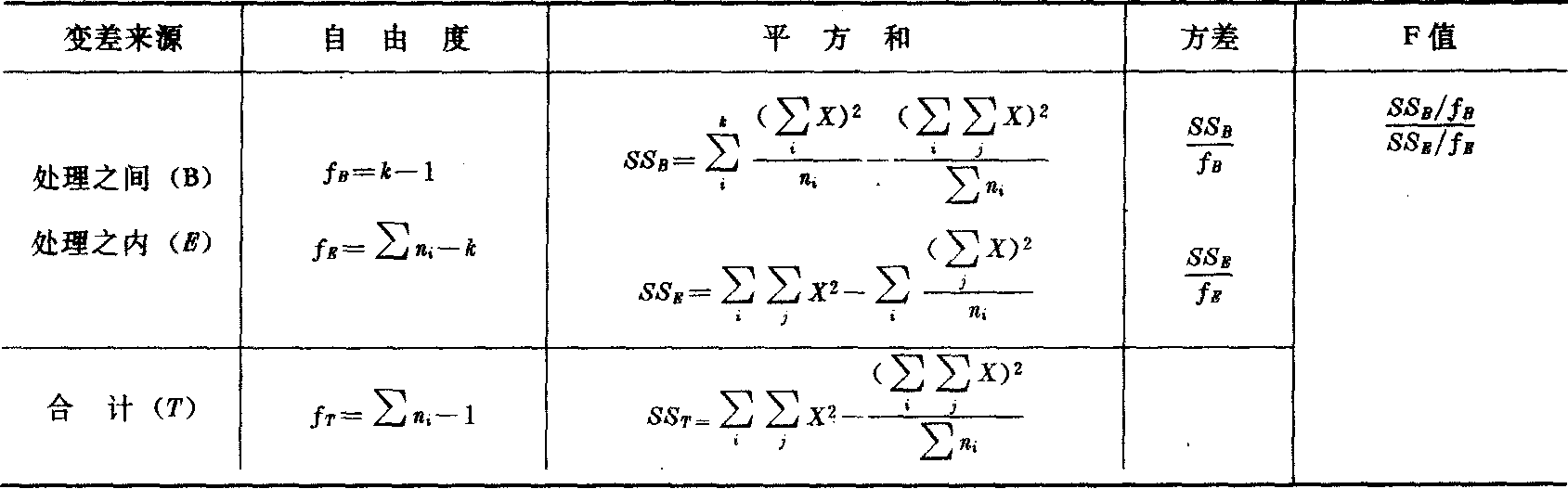
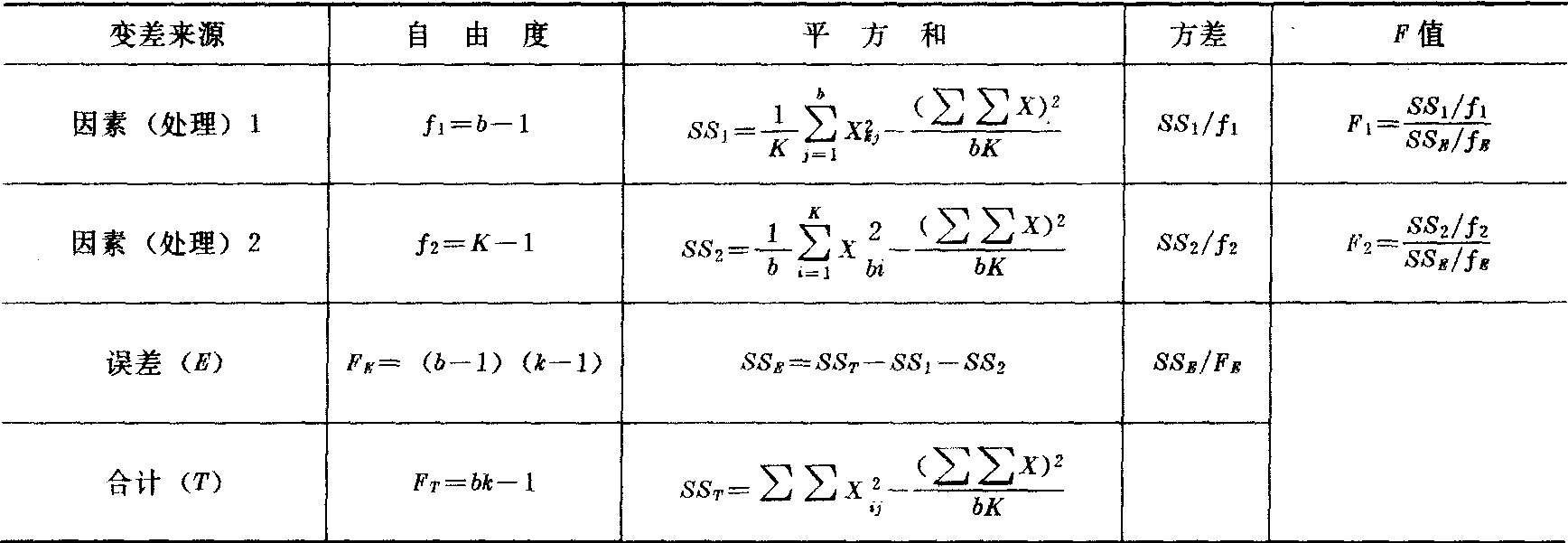
双因素的方差分析(见表3与表4)
表3 双因素方差分析的记数法

双因素方差分析表

表4=H₀:u₁＝u₂＝…=u_k,H′₀: u′₁＝u′₂＝…= μ′_k

其他方差分析都可按表2和表4的基本思路来处理。此后不一一累述。

方差分析analysis of variance

将包含k个样本(一般k≥3)的试验观察值总变异的平方和与自由度分解为不同变异来源的平方和与自由度，求得各变异来源的总体方差估值，计算适当的F值以测验各样本是否具有相同的总体均值。即测验H₀:μ₁＝μ₂＝…=μk=μ，或记作μi=μ(i=1,2，…，k)是否成立的统计推断方法。对于不同设计的试验资料应采用不同的方差分析方法。这里介绍两种最基本的方差分析方法。
单向分组资料的方差分析 研究一个因素A的不同水平对所考察对象的影响，A取k个水平A_i(其分

❸给出显著水平a。

❹由F分布查自由度为k-1,n-k的F分布上a分位数Fa。

❺列统计量计算表(表1)。

❻列方差分析表(表2)。

表1 单向分组资料方差分析统计量计算表

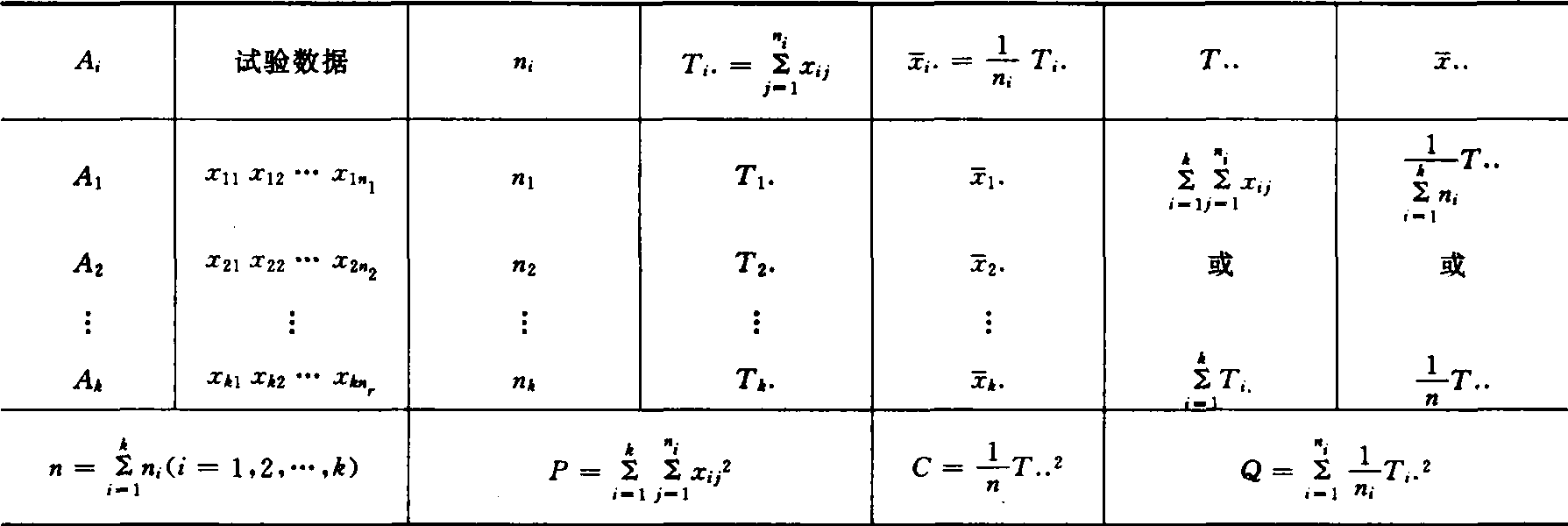
表2 单向分组资料方差分析表

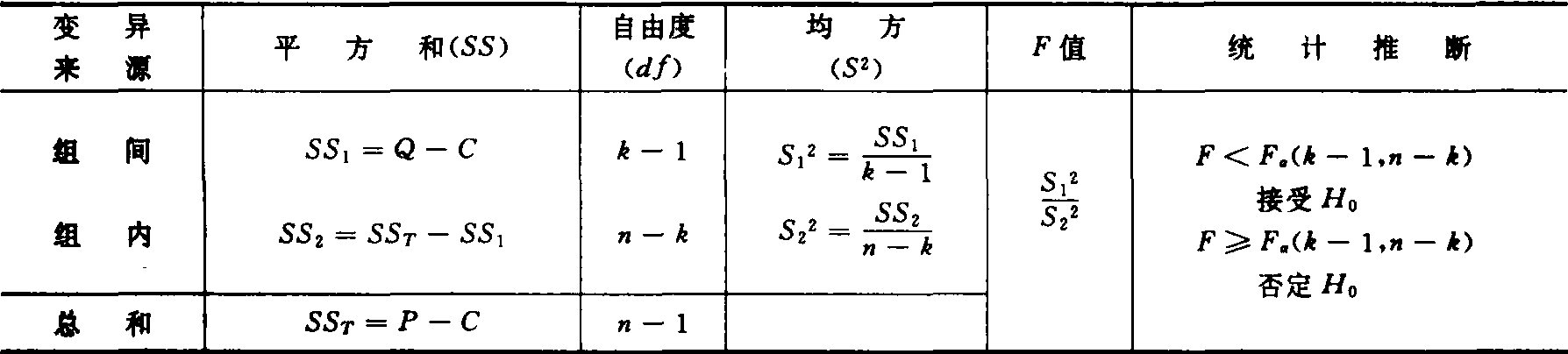
双向分组资料的方差分析 单因素完全随机区组设计试验（参见随机区组设计）中，区组看作一个试验因素，若试验因素A取k个水平，区组数（重复数）为n则所得试验数据{x_ij}(i=1,2，…，k;j=1,2，…，n)符合k行，n列双向分组资料模式(如表3)。检验因素A的效应或区组效应对试验结果有无显著影响，其步骤如下：
❶假设H₀,A因素效应对试验结果无显著影响，即μ_i＝μ(i=1,2，…，k)或区组效应对试验结果无显著影响，即μ_j＝μ(j=1,2，…，n)。

❷确定统计量并明确其分布

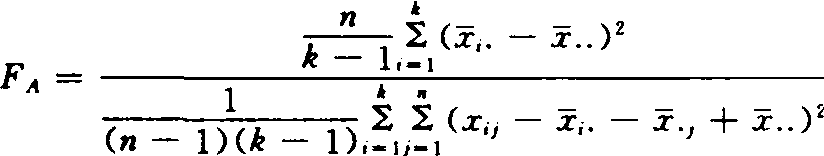
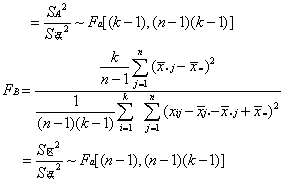
❸给出显著水平α

❹查F表得Fa[(k-1,(n-1)(k-1)]和Fa[(n-1),(n-1)(k-1)]值

❺列表计算统计量(表3)

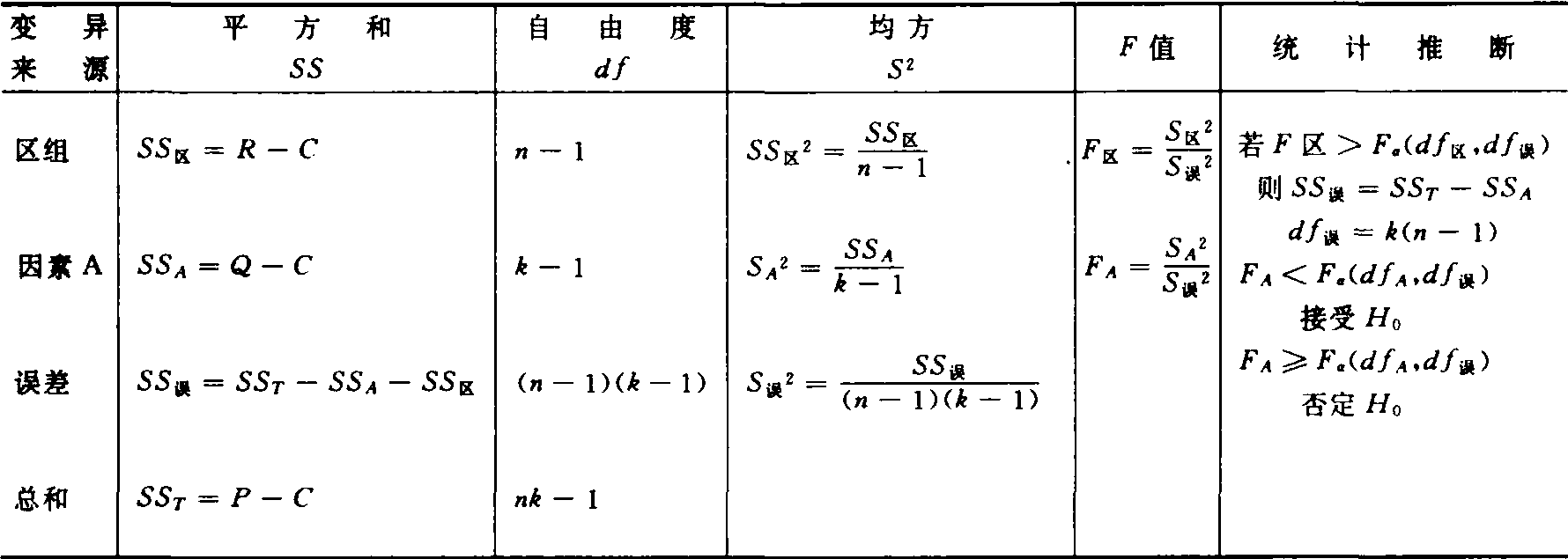
❻列方差分析表(表4)

表3 双向分组资料方差分析统计量计算表

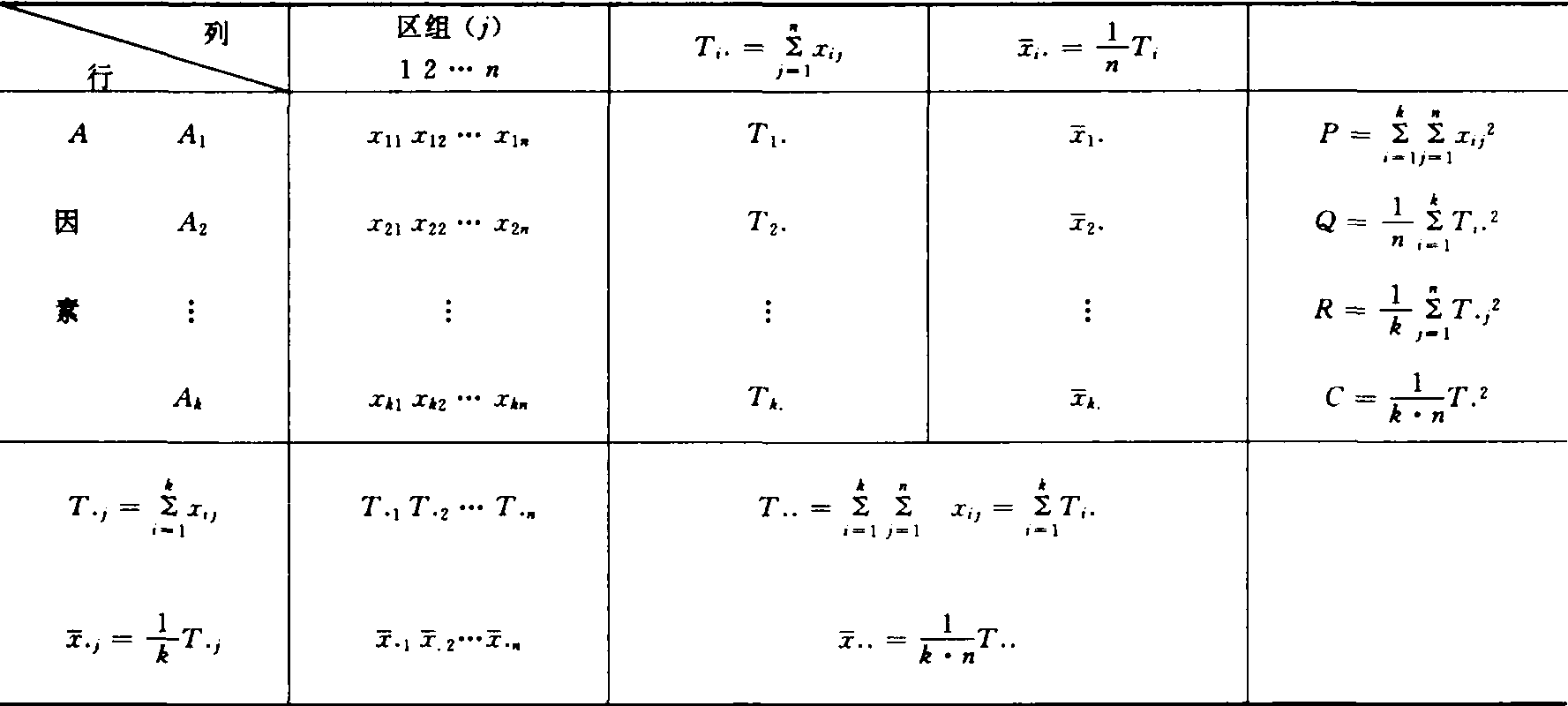
表4 双向分组资料方差分析表