方程组的同解变形定理fangchengzu de tongjie bianxingdingli

包括：
定理1 若方程组里的任何一个方程用与它同解的方程来代替，则所得方程组与原方程组同解.
例如，解方程组

将方程(1)用它的同解方程3x-2y=6代替所得方程组

与原方程组同解.
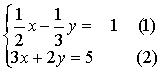
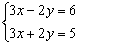
定理2 若方程组中的一个方程是一个未知数(比如y)用另一个（或另一些）未知数(比如x或其他)的代数式来表示的等式，在这方程组的另一个（或另一些）方程里，把y用x（或其他）的代数式代替，则所得方程组与原方程组同解.若以二元方程组来表示此定理，即方程组

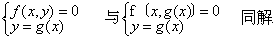
这个定理是代入消元法解方程组的理论依据.例如，解方程组

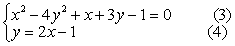
根据本定理可化为解与它同解的方程组

这样由(5)可求出x的值，再将求得的x的值代入(4)求出对应的y值.从而得到方程组的解.这个定理是用代入消元法解第Ⅰ类型（由一个一次方程和一个二次方程组成的）二元二次方程组时，在求出一个未知数的值之后必须代入一次方程去求对应的另一个未知数的值的理论依据.
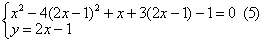
定理3 若把方程组里的一些方程的两边分别相加（或加减）得出一个新方程，并且把方程组参加运算的任意一个方程用这个新方程代替，而其余方程不变，所得方程组与原方程组同解.
这个定理是加减消元法的理论依据.例如解方程组

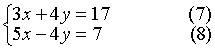
依据本定理可化为解与它同解的方程组

或

其中方程(9)是由方程(7)、(8)两边分别相加得到的新方程.
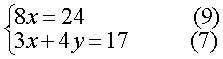
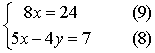
定理4 若方程组中的一个方程可以变形成一边为几个因式之积，另一边为零的形式，则令这几个因式各自为零所得的几个方程分别与原方程组的其余方程联立而成的几个新方程组与原方程组同解.
例如，解方程组

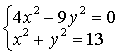
原方程组即

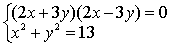
据本定理可化作解下列两个方程组