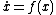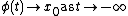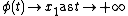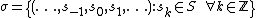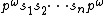- Symbolic dynamics
- See also
- References
In mathematics, in the phase portrait of a dynamical system, a heteroclinic orbit (sometimes called a heteroclinic connection) is a path in phase space which joins two different equilibrium points. If the equilibrium points at the start and end of the orbit are the same, the orbit is a homoclinic orbit.
Consider the continuous dynamical system described by the ODE
Suppose there are equilibria at  and
and 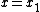 , then a solution
, then a solution  is a heteroclinic orbit from
is a heteroclinic orbit from  to
to 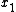 if
if
and
This implies that the orbit is contained in the stable manifold of 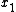 and the unstable manifold of
and the unstable manifold of  .
.
Symbolic dynamics
By using the Markov partition, the long-time behaviour of hyperbolic system can be studied using the techniques of symbolic dynamics. In this case, a heteroclinic orbit has a particularly simple and clear representation. Suppose that  is a finite set of M symbols. The dynamics of a point x is then represented by a bi-infinite string of symbols
is a finite set of M symbols. The dynamics of a point x is then represented by a bi-infinite string of symbols
A periodic point of the system is simply a recurring sequence of letters. A heteroclinic orbit is then the joining of two distinct periodic orbits. It may be written as
where 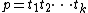 is a sequence of symbols of length k, (of course,
is a sequence of symbols of length k, (of course, 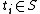 ), and
), and  is another sequence of symbols, of length m (likewise,
is another sequence of symbols, of length m (likewise, 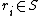 ). The notation
). The notation 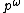 simply denotes the repetition of p an infinite number of times. Thus, a heteroclinic orbit can be understood as the transition from one periodic orbit to another. By contrast, a homoclinic orbit can be written as
simply denotes the repetition of p an infinite number of times. Thus, a heteroclinic orbit can be understood as the transition from one periodic orbit to another. By contrast, a homoclinic orbit can be written as
with the intermediate sequence  being non-empty, and, of course, not being p, as otherwise, the orbit would simply be
being non-empty, and, of course, not being p, as otherwise, the orbit would simply be 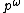 .
.
See also
- Heteroclinic connection
- Heteroclinic cycle
- Heteroclinic bifurcation
- Homoclinic orbit
References
- John Guckenheimer and Philip Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, (Applied Mathematical Sciences Vol. 42), Springer
- Murder Most Unladylike
- Murder Mountain (disambiguation)
- Murder Mountain (TV series)
- Murder-mystery
- Murder, Mystery, and My Family
- Murder Mystery (film)
- Murder Mystery (Schitt's Creek)
- Murder Mystery (upcoming film)
- Murder Nature
- Murder of 2Pac
- Murder of Aaron Pajich
- Murder of Aaron Pajich-Sweetman
- Murder of Aaron Sweetman
- Murder of Abdurrahim Özüdoğru
- Murder of Adria Sauceda
- Murder of A. F. M. Rezaul Karim Siddique
- Murder of Aiia Maasarwe
- Murder of Alayna Ertl
- Murder of Albert McColl
- Murder of Alesha MacPhail
- Murder of Alexandra Mezher
- Murder of Alfred Lingle
- Murder of Alicia Reynolds
- Murder of Alison Parker
- Murder of Alison Parker and Adam Ward