- Algorithm information
- Algorithm description
- Example
- See also
- References
In computer science, Hirschberg's algorithm, named after its inventor, Dan Hirschberg, is a dynamic programming algorithm that finds the optimal sequence alignment between two strings. Optimality is measured with the Levenshtein distance, defined to be the sum of the costs of insertions, replacements, deletions, and null actions needed to change one string into the other. Hirschberg's algorithm is simply described as a more space efficient version of the Needleman–Wunsch algorithm that uses divide and conquer.[1] Hirschberg's algorithm is commonly used in computational biology to find maximal global alignments of DNA and protein sequences.
Algorithm information
Hirschberg's algorithm is a generally applicable algorithm for optimal sequence alignment. BLAST and FASTA are suboptimal heuristics. If x and y are strings, where length(x) = n and length(y) = m, the Needleman-Wunsch algorithm finds an optimal alignment in O(nm) time, using O(nm) space. Hirschberg's algorithm is a clever modification of the Needleman-Wunsch Algorithm which still takes O(nm) time, but needs only O(min{n,m}) space and is much faster in practice.[2]
One application of the algorithm is finding sequence alignments of DNA or protein sequences. It is also a space-efficient way to calculate the longest common subsequence between two sets of data such as with the common diff tool.
The Hirschberg algorithm can be derived from the Needleman-Wunsch algorithm by observing that:[3]
- one can compute the optimal alignment score by only storing the current and previous row of the Needleman-Wunsch score matrix;
- if
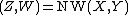 is the optimal alignment of
is the optimal alignment of  , and
, and 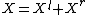 is an arbitrary partition of
is an arbitrary partition of  , there exists a partition
, there exists a partition 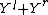 of
of  such that
such that 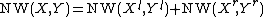 .
.
Algorithm description
 denotes the i-th character of
denotes the i-th character of  , where
, where  .
. 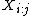 denotes a substring of size
denotes a substring of size 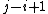 , ranging from i-th to the j-th character of
, ranging from i-th to the j-th character of  .
. 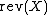 is the reversed version of
is the reversed version of  .
.
 and
and  are sequences to be aligned. Let
are sequences to be aligned. Let  be a character from
be a character from  , and
, and  be a character from
be a character from  . We assume that
. We assume that 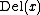 ,
, 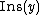 and
and 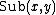 are well defined integer-valued functions. These functions represent the cost of deleting
are well defined integer-valued functions. These functions represent the cost of deleting  , inserting
, inserting  , and replacing
, and replacing  with
with  , respectively.
, respectively.
We define 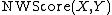 , which returns the last line of the Needleman-Wunsch score matrix
, which returns the last line of the Needleman-Wunsch score matrix 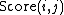 :
:
'''function''' NWScore(X,Y) Score(0,0) = 0 // 2*length(Y) array '''for''' j=1 '''to''' length(Y) Score(0,j) = Score(0,j-1) + Ins(Yj) '''for''' i=1 '''to''' length(X) //init array Score(1,0) = Score(0,0) + Del(Xi) '''for''' j=1 '''to''' length(Y) scoreSub = Score(0,j-1) + Sub(Xi, Yj) scoreDel = Score(0,j) + Del(Xi) scoreIns = Score(1,j-1) + Ins(Yj) Score(1,j) = max(scoreSub, scoreDel, scoreIns) '''end''' //copy Score[1] to Score[0] Score(0,:) = Score(1,:) '''end''' '''for''' j=0 '''to''' length(Y) LastLine(j) = Score(1,j) '''return''' LastLine
Note that at any point, 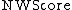 only requires the two most recent rows of the score matrix. Thus,
only requires the two most recent rows of the score matrix. Thus, 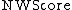 is implemented in
is implemented in 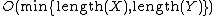 space
space
The Hirschberg algorithm follows:
'''function''' Hirschberg(X,Y) Z = "" W = "" '''if''' length(X) == 0 '''for''' i=1 '''to''' length(Y) Z = Z + '-' W = W + Yi '''end''' '''else if''' length(Y) == 0 '''for''' i=1 '''to''' length(X) Z = Z + Xi W = W + '-' '''end''' '''else if''' length(X) == 1 '''or''' length(Y) == 1 (Z,W) = NeedlemanWunsch(X,Y) '''else''' xlen = length(X) xmid = length(X)/2 ylen = length(Y) ScoreL = NWScore(X1:xmid, Y) ScoreR = NWScore(rev(Xxmid+1:xlen), rev(Y)) ymid = arg max ScoreL + rev(ScoreR) (Z,W) = Hirschberg(X1:xmid, y1:ymid) + Hirschberg(Xxmid+1:xlen, Yymid+1:ylen) '''end''' '''return''' (Z,W)
In the context of Observation (2), assume that 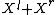 is a partition of
is a partition of  . Index
. Index 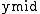 is computed such that
is computed such that 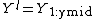 and
and 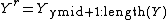 .
.
Example
Let
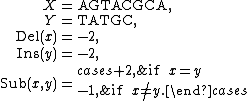
The optimal alignment is given by
W = AGTACGCA Z = --TATGC-
Indeed, this can be verified by backtracking its corresponding Needleman-Wunsch matrix:
'''T A T G C''' '''0''' -2 -4 -6 -8 -10 '''A''' '''-2''' -1 0 -2 -4 -6 '''G''' '''-4''' -3 -2 -1 0 -2 '''T''' -6 '''-2''' -4 0 -2 -1 '''A''' -8 -4 '''0''' -2 -1 -3 '''C''' -10 -6 -2 '''-1''' -3 1 '''G''' -12 -8 -4 -3 '''1''' -1 '''C''' -14 -10 -6 -5 -1 '''3''' '''A''' -16 -12 -8 -7 -3 '''1'''
One starts with the top level call to 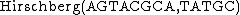 , which splits the first argument in half:
, which splits the first argument in half: 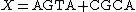 . The call to
. The call to 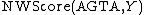 produces the following matrix:
produces the following matrix:
'''T A T G C''' 0 -2 -4 -6 -8 -10 '''A''' -2 -1 0 -2 -4 -6 '''G''' -4 -3 -2 -1 0 -2 '''T''' -6 -2 -4 0 -2 -1 '''A''' -8 -4 0 -2 -1 -3
Likewise, 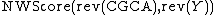 generates the following matrix:
generates the following matrix:
'''C G T A T''' 0 -2 -4 -6 -8 -10 '''A''' -2 -1 -3 -5 -4 -6 '''C''' -4 0 -2 -4 -6 -5 '''G''' -6 -2 2 0 -2 -4 '''C''' -8 -4 0 1 -1 -3
Their last lines (after reversing the latter) and sum of those are respectively
ScoreL = [ -8 -4 0 -2 -1 -3 ] rev(ScoreR) = [ -3 -1 1 0 -4 -8 ] Sum = [-11 -5 '''1''' -2 -5 -11]
The maximum (shown in bold) appears at ymid = 2, producing the partition  .
.
The entire Hirschberg recursion (which we omit for brevity) produces the following tree:
(AGTACGCA,TATGC) / \\ (AGTA,TA) (CGCA,TGC) / \\ / \\ (AG, ) (TA,TA) (CG,TG) (CA,C) / \\ / \\ (T,T) (A,A) (C,T) (G,G)
The leaves of the tree contain the optimal alignment.
See also
- Longest Common Subsequence
References
2. ^http://www.cs.tau.ac.il/~rshamir/algmb/98/scribe/html/lec02/node10.html
3. ^{{cite journal|last=Hirschberg|first=D. S.|authorlink=Dan Hirschberg|title=A linear space algorithm for computing maximal common subsequences|journal=Communications of the ACM|volume=18|issue=6|year=1975|pages=341–343|doi=10.1145/360825.360861|mr=0375829|citeseerx=10.1.1.348.4774}}
- Rajkot-Somnath line
- Rajkot - Somnath Passenger
- Rajkot Taluka
- Rajkot - Veraval Express
- Rajkot-Veraval high-speed rail corridor
- Rajkot - Veraval Passenger
- Rajkot-Wankaner section
- Rajkot West (Vidhan Sabha constituency)
- Rajkov
- Rajković (Mionica)
- Rajković, Mionica
- Rajko Čubrić
- Rajko Žinzifov
- Raj K. Purohit
- Raj Krishna Dawn
- Rajk trial
- Rajkumar Baisla
- Rajkumar Baisla (Wrestler)
- Rajkumar Barjatya
- Rajkumar Buyya
- Raj Kumar Goel Engineering College
- Rajkumar Hirani Films
- Rajkumari Amrit Kaur College of Nursing
- Rajkumari Banerji
- Rajkumari Devi