不定积分的第二换元积分法budingjifen de dierhuanyuan jifenfa
设函数x =φ(x)单调、可导,且ψ′(t)≠0,又设f[ψ(t)〕ψ′(t)具有原函数φ(t),则根据换元公式
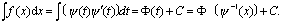
第二换元积分法的基本思路:若∫ f(x)dx不易求,可适当选择x = ψ(t),将原不定积分化为
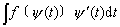 的形式;而
的形式;而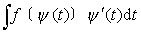 容易求出,且等于ψ(t) +C,则可根据上述法则,通过反函数关系,将ψ(t)+C还原为F[ψ-1(x)]+C,从而得到所求的结果.这里选择ψ(t)的条件是:❶ψ(t)单调,可导,且+ψ′(t)≠0,以保证上述法则成立且被积函数f(x)的定义域不变.
容易求出,且等于ψ(t) +C,则可根据上述法则,通过反函数关系,将ψ(t)+C还原为F[ψ-1(x)]+C,从而得到所求的结果.这里选择ψ(t)的条件是:❶ψ(t)单调,可导,且+ψ′(t)≠0,以保证上述法则成立且被积函数f(x)的定义域不变.❷要使∫f(ψ(t)]ψ′ (t)dt 容易求.
第二换元积分法用来求几种常见的无理函数的积分,十分方便.
❶若被积函数含有因子
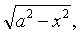 则可令x =asint或x =a c ost;
则可令x =asint或x =a c ost;❷若被积函数含有因子
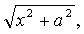 则可令x =atgt;
则可令x =atgt;❸若被积函数含有因子
 则可令x =aseet.
则可令x =aseet.例 求
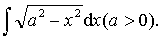
解 令x=asint,则ex=acostdt,t=aresin x/a. a
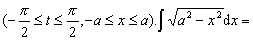
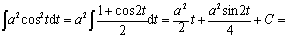
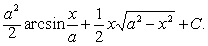
- ConnecticutWits
- connective tissue
- Connelly,Marc
- Connemara
- Connolly,Cyril Vernon
- Connolly,James
- Connolly,Maureen
- Connors,Jimmy
- conodont
- conquistador
- Conrad
- Conrad
- Conrad I
- Conrad Ⅱ
- Conrad Ⅲ
- Conrad Ⅳ
- Conrad,Joseph
- consanguinity
- conscience
- Conscience,Hendrik
- consciousness
- Consejo Real
- consensus
- Consentes Dii
- consent,popular