标准差biaozhun cha
差异量数之一。由变异数(又称方差)的平方根得来,故又称均方差。样本标准差用S或SD表示,总体标准量用σ表示。计算标准差的公式是:
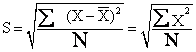
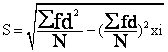
标准差Biaozhuncha
是每个数据与平均数之差的平方的算术平均数的平方根。是表示数据离中趋势的最常用的量数,一般以S表示。计算公式为:
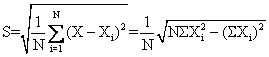
标准差
又称“均方差”。各单位标志值与平均数离差的平方的算术平均数的平方根。测定标志变异度的最主要指标。计算公式为:
![]()
标准差
方差的算术根。常用σ表示,即σ=![]() 。其估计值为Sn=
。其估计值为Sn=![]() 或S=
或S=![]() 。常被应用于测验分数统计中。
。常被应用于测验分数统计中。
标准差standard deviation
统计学上指方差的平方根值。表现一组变数的变异度。其单位与观察值的度量单位相同。样本标准差的表达式为:
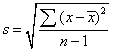
 )2为离均差的平方和,简称平方和;n-1称为自由度。样本标准差是总体标准差的估计值。总体标准差以σ表示。
)2为离均差的平方和,简称平方和;n-1称为自由度。样本标准差是总体标准差的估计值。总体标准差以σ表示。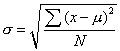
- 中国华源集团
- 中国华电集团公司工程建设安全文明施工标准化配置手册
- 中国华电集团公司工程建设项目法人管理手册
- 中国华能集团公司四川分公司
- 中国华西企业公司
- 中国华西工程设计建设总公司
- 中国协和医科大学
- 中国卒中后抑郁障碍规范化诊疗指南
- 中国单位或个人向外国申请专利的办法
- 中国南动集团财务公司
- 中国南岳衡山国际寿文化节
- 中国南方农村人口理论研讨会
- 中国南方出土商周铜铙概论
- 中国南方干栏及其变迁
- 中国南方果树
- 中国南方民族史志要籍题解
- 中国南方淡水鱼类原色图鉴
- 中国南方航空集团公司
- 中国南极和南大洋考察
- 中国南极考察中山站
- 中国南极考察长城站
- 中国南极长城站
- 中国南水北调东线工程
- 中国南水北调中线工程
- 中国南水北调工程