树shu

一类非常重要的非线性数据结构.树是以分支关系定义的层次结构，在树结构中，袭用了自然界中树的一些术语，如树根、树枝和树叶.举例来说，在对学校进行学生管理时，常常把学校分成年级，年级又分成班，逐级进行管理，构成如图1所示的分支层次结构，象一棵倒置的树.树是由一些“结点”和“树枝”组成的.学校这个结点比较特殊，在它的上面不再有其它结点，称其为“根”.各班下面再没有其他结点了，称其为“树叶”.从层次上看，学校为第1层，年级为第2层，班为第3层.本例中共有3层，因此其树的深度为3.两个结点之间的联接关系用树枝表示.每个树枝连接着上下两个结点，上面的结点称“双亲”结点，下面的结点称“子女”结点，同一个结点的“子女”之间互称“兄弟”结点.如一年级结点是11班结点、12班结点、13班结点的“双亲”；11班结点与12班结点、13班结点之间互称“兄弟”.
学校结点有三棵子树，分别为：
T₁＝{一年级，11班，12班，13班}
T₂＝ {二年级，21班，22班}
T₃＝{三年级，31班，32班}
称T₁,T₂,T₃为学校这个根结点的子树.而一年级结点是T₁的根，二年级结点是T₂的根，三年级结点是T₃的根.
一个结点所具有的子树的数目，称为该结点的度.学校结点的度数为3，二年级结点的度数为2.
树在计算机中可用多重链表来表示：每个结点除有一个数据域外，还有n个指针域，n的数目取决于该结点的子女数.指针的作用是指明子女结点的存储单元，它将两个有“血缘”关系的结点联接起来.结点的一般表示为：

数据

指针1

指针2

……

指针n

将图1用多重链表画出的逻辑结构如图2所示.每个结点有一个数据域，有3个指针域.如果某个结点只有两个子女，则会有一个指针域是空余的，这时放入一个符号“∧”表示无指针.如果某个结点三个指针域都是空的，则说明，它没有子女，或者说它是“树叶”.
每个结点只有两个子女的树称为二叉树，这类树应用最广泛.
在计算机高级语言的编译过程中，在生成代码之前，常常要将语句和算术表达式分解为树结构，以便于处理；在模块程序设计中，需将各个模块组织成树形结构，形成层次，以简化模块间的接口关系；在数据处理中，把数据组织成树结构可以大大提高查找速度；解人工智能问题，一些决策过程都会使用树结构.

树shu

连通的无回路的无向图.树中度数为1的点称为树叶，度数大于1的点称为分支点.无回路的无向图称为（森）林，它的每个连通分支都是树.如图

是所有六点的不同构的树.
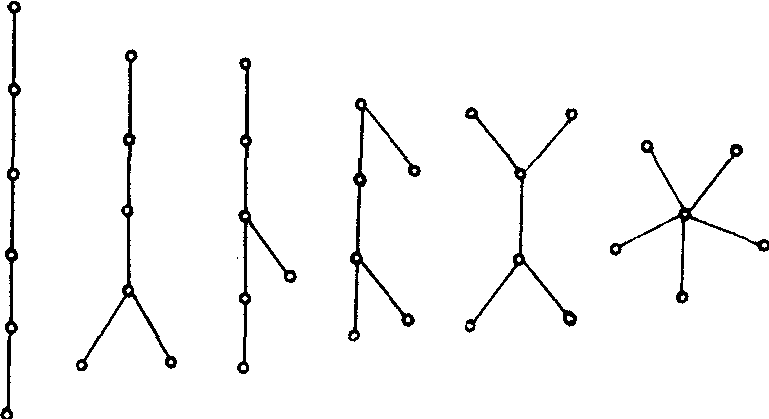
定理：任意n(≥2)点的树至少有两片树叶.
定理：设图T有n个点，m条边，则以下几个条件互相等价：
❶T连通无回路，即T是树；

❷T无回路，且m=n-1;

❸T连通，且m=n-1;

❹T无回路，但任意增加一边，则得到一条且仅一条回路；

❺T连通，但删去任一边后不连通；

❻T的每一对点之间有一条且仅一条路.
这里，条件
❹指出树是边数最多的无回路的图；而
❺指出树是边数最少的连通图.
若图G= 〈V,E〉的生成子图T是树，则T称为G的生成树.图G有生成树当且仅当G是连通图.
利用“破回路法”可求给定连通图的生成树.这仅需每次删去一条回路上的一条边（保留端点），直到不再含有回路为止，就得到一棵生成树.
利用“破回路法”可求给定连通图的生成树.只需从任一边开始，每次增加一边，但要求加进来的边与已选好的边不构成回路，直到包含所有点为止.
对连通赋权图G来说，若T是生成树，T的所有边的权的和，称为T的树权，记做W (T).在G中的树权最小的生成树，称为G的最小生成树.
例如，点表示城市，边表示城市间的电话线，边的权为电路的造价.则选取最小生成树有重要经济意义.用克鲁斯卡尔算法产生最小生成树：
❶选取G的最小权边e₁(有多条时，任选一条);

❷设已选好e₁,e₂，…，ei，在G中选取不同于e₁,e₂，…，e_i的边e_i+1，使得e₁,e₂，…，e_i,e_i+1不构成回路，并且e_i+1是满足此条件的最小权边(有多条时，任选一条);

❸i=n-1 (n为G的点数)时，算法终止.