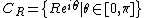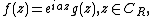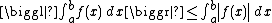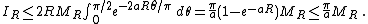“Jordan's lemma”的意思、由来-开放百科全书

词条

Jordan's lemma

释义

Statement
Remarks
Application of Jordan's lemma
Example
Proof of Jordan's lemma
See also
References

In complex analysis, Jordan's lemma is a result frequently used in conjunction with the residue theorem to evaluate contour integrals and improper integrals. It is named after the French mathematician Camille Jordan.

Statement

Consider a complex-valued, continuous function {{math|f}}, defined on a semicircular contour

of positive radius {{math|R}} lying in the upper half-plane, centred at the origin. If the function {{math|f}} is of the form

with a positive parameter {{math|a}}, then Jordan's lemma states the following upper bound for the contour integral:

where equal sign is when {{math|g}} vanishes everywhere{{clarify|date=October 2017}}. An analogous statement for a semicircular contour in the lower half-plane holds when {{math|a < 0}}.

Remarks

If {{math|f}} is continuous on the semicircular contour {{math|C_R}} for all large {{math|R}} and

{{NumBlk|::|

|{{EquationRef|*}}}}

then by Jordan's lemma

For the case {{math|a {{=}} 0}}, see the estimation lemma.
Compared to the estimation lemma, the upper bound in Jordan's lemma does not explicitly depend on the length of the contour {{math|C_R}}.

Application of Jordan's lemma

Jordan's lemma yields a simple way to calculate the integral along the real axis of functions {{math|f(z) {{=}} e^{i a z} g(z)}} holomorphic on the upper half-plane and continuous on the closed upper half-plane, except possibly at a finite number of non-real points {{math|z₁}}, {{math|z₂}}, …, {{math|z_n}}. Consider the closed contour {{math|C}}, which is the concatenation of the paths {{math|C₁}} and {{math|C₂}} shown in the picture. By definition,

Since on {{math|C₂}} the variable {{math|z}} is real, the second integral is real:

The left-hand side may be computed using the residue theorem to get, for all {{math|R}} larger than the maximum of {{math|{{!}}z₁{{!}}}}, {{math|{{!}}z₂{{!}}}}, …, {{math|{{!}}z_n{{!}}}},

where {{math|Res(f, z_k)}} denotes the residue of {{math|f}} at the singularity {{math|z_k}}. Hence, if {{math|f}} satisfies condition ({{EquationNote|*}}), then taking the limit as {{math|R}} tends to infinity, the contour integral over {{math|C₁}} vanishes by Jordan's lemma and we get the value of the improper integral

Example

The function

satisfies the condition of Jordan's lemma with {{math|a {{=}} 1}} for all {{math|R > 0}} with {{math|R ≠ 1}}. Note that, for {{math|R > 1}},

hence ({{EquationNote|*}}) holds. Since the only singularity of {{math|f}} in the upper half plane is at {{math|z {{=}} i}}, the above application yields

Since {{math|z {{=}} i}} is a simple pole of {{math|f}} and {{math|1 + z² {{=}} (z + i)(z − i)}}, we obtain

so that

This result exemplifies the way some integrals difficult to compute with classical methods are easily evaluated with the help of complex analysis.

Proof of Jordan's lemma

By definition of the complex line integral,

Now the inequality

yields

Using {{math|M_R}} as defined in ({{EquationNote|*}}) and the symmetry {{math|sin θ {{=}} sin(π – θ)}}, we obtain

Since the graph of {{math|sin θ}} is concave on the interval {{math|θ ∈ [0, π ⁄ 2]}}, the graph of {{math|sin θ}} lies above the straight line connecting its endpoints, hence

for all {{math|θ ∈ [0, π ⁄ 2]}}, which further implies

References

{{Cite book| last1=Brown| first1=James W.| last2=Churchill| first2=Ruel V.| date=2004| title=Complex Variables and Applications| edition=7th|place=New York | publisher=McGraw Hill| pages=262–265| isbn = 0-07-287252-7}}

3 : Theorems in complex analysis|Articles containing proofs|Lemmas

随便看