“King's graph”的意思、由来-开放百科全书

In graph theory, a king's graph is a graph that represents all legal moves of the king chess piece on a chessboard where each vertex represents a square on a chessboard and each edge is a legal move. More specifically, an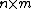

king's graph is a king's graph of an

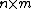chessboard.^[1] It is the map graph formed from the squares of a chessboard by making a vertex for each square and an edge for each two squares that share an edge or a corner. It can also be constructed as the strong product of two path graphs.^[2]

For a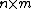

king's graph the total number of vertices is

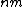and the number of edges is

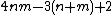. For a square

king's graph, the total number of vertices is

and the total number of edges is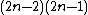

.^[3]

The neighbourhood of a vertex in the king's graph corresponds to the Moore neighborhood for cellular automata.^[4]

A generalization of the king's graph, called a kinggraph, is formed from a squaregraph (a planar graph in which each bounded face is a quadrilateral and each interior vertex has at least four neighbors) by adding the two diagonals of every quadrilateral face of the squaregraph.^[5]

References

1. ^{{citation | last = Chang | first = Gerard J. | editor1-last = Du | editor1-first = Ding-Zhu | editor2-last = Pardalos | editor2-first = Panos M. | contribution = Algorithmic aspects of domination in graphs | location = Boston, MA | mr = 1665419 | pages = 339–405 | publisher = Kluwer Acad. Publ. | title = Handbook of combinatorial optimization, Vol. 3 | year = 1998}}. Chang defines the king's graph on [https://books.google.com/books?id=w0rmms0_hMMC&pg=PA341 p. 341].
2. ^{{citation | last1 = Berend | first1 = Daniel | last2 = Korach | first2 = Ephraim | last3 = Zucker | first3 = Shira | contribution = Two-anticoloring of planar and related graphs | contribution-url = http://www.emis.ams.org/journals/DMTCS/pdfpapers/dmAD0130.pdf | location = Nancy | mr = 2193130 | pages = 335–341 | publisher = Association for Discrete Mathematics & Theoretical Computer Science | series = Discrete Mathematics & Theoretical Computer Science Proceedings | title = 2005 International Conference on Analysis of Algorithms | year = 2005}}.
3. ^{{Cite OEIS|A002943}}
4. ^{{citation | last = Smith | first = Alvy Ray | authorlink = Alvy Ray Smith | contribution = Two-dimensional formal languages and pattern recognition by cellular automata | doi = 10.1109/SWAT.1971.29 | pages = 144–152 | title = 12th Annual Symposium on Switching and Automata Theory | year = 1971}}.
5. ^{{citation | last1 = Chepoi | first1 = Victor | last2 = Dragan | first2 = Feodor | last3 = Vaxès | first3 = Yann | contribution = Center and diameter problems in plane triangulations and quadrangulations | pages = 346–355 |isbn=0-89871-513-X |chapterurl=http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1.7694&rep=rep1&type=pdf | title = Proceedings of the Thirteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '02) | year = 2002}}.

References

See also