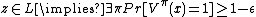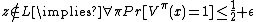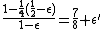请输入您要查询的百科知识：

　

词条 MAX-3SAT
释义

  1. Approximability

  2. Theorem 1 (inapproximability)

  3. Theorem 2

  4. References

MAX-3SAT is a problem in the computational complexity subfield of computer science. It generalises the Boolean satisfiability problem (SAT) which is a decision problem considered in complexity theory. It is defined as:

Given a 3-CNF formula Φ (i.e. with at most 3 variables per clause), find an assignment that satisfies the largest number of clauses.

MAX-3SAT is a canonical complete problem for the complexity class MAXSNP (shown complete in Papadimitriou pg. 314).

Approximability

The decision version of MAX-3SAT is NP-complete. Therefore, a polynomial-time solution can only be achieved if P = NP. An approximation within a factor of 2 can be achieved with this simple algorithm, however:

  • Output the solution in which most clauses are satisfied, when either all variables = TRUE or all variables = FALSE.
  • Every clause is satisfied by one of the two solutions, therefore one solution satisfies at least half of the clauses.

The Karloff-Zwick algorithm runs in polynomial-time and satisfies ≥ 7/8 of the clauses.

Theorem 1 (inapproximability)

The PCP theorem implies that there exists an ε > 0 such that (1-ε)-approximation of MAX-3SAT is NP-hard.

Proof:

Any NP-complete problem {{tmath|L \\in \\mathsf{PCP}(O(\\log (n)), O(1))}} by the PCP theorem. For x ∈ L, a 3-CNF formula Ψx is constructed so that

  • x ∈ L ⇒ Ψx is satisfiable
  • x ∉ L ⇒ no more than (1-ε)m clauses of Ψx are satisfiable.

The Verifier V reads all required bits at once i.e. makes non-adaptive queries. This is valid because the number of queries remains constant.

  • Let q be the number of queries.
  • Enumerating all random strings Ri ∈ V, we obtain poly(x) strings since the length of each string .
  • For each Ri
    • V chooses q positions i1,...,iq and a Boolean function fR: {0,1}q->{0,1} and accepts if and only if fR(π(i1,...,iq)). Here π refers to the proof obtained from the Oracle.

Next we try to find a Boolean formula to simulate this. We introduce Boolean variables x1,...,xl, where l is the length of the proof. To demonstrate that the Verifier runs in Probabilistic polynomial-time, we need a correspondence between the number of satisfiable clauses and the probability the Verifier accepts.

  • For every R, add clauses representing fR(xi1,...,xiq) using 2q SAT clauses. Clauses of length q are converted to length 3 by adding new (auxiliary) variables e.g. x2 ∨ x10 ∨ x11 ∨ x12 = ( x2 ∨ x10 ∨ yR) ∧ ( {{overline|y}}R ∨ x11 ∨ x12). This requires a maximum of q2q 3-SAT clauses.
  • If z ∈ L then
    • there is a proof π such that Vπ (z) accepts for every Ri.
    • All clauses are satisfied if xi = π(i) and the auxiliary variables are added correctly.
  • If input z ∉ L then
    • For every assignment to x1,...,xl and yR's, the corresponding proof π(i) = xi causes the Verifier to reject for half of all R ∈ {0,1}r(|z|).
    • For each R, one clause representing fR fails.
    • Therefore a fraction 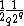of clauses fails.

It can be concluded that if this holds for every NP-complete problem then the PCP theorem must be true.

Theorem 2

Håstad [1] demonstrates a tighter result than Theorem 1 i.e. the best known value for ε.

He constructs a PCP Verifier for 3-SAT that reads only 3 bits from the Proof.

For every ε > 0, there is a PCP-verifier M for 3-SAT that reads a random string r of length {{tmath|O(\\log(n))}} and computes query positions ir, jr, kr in the proof π and a bit br. It accepts if and only if

π(ir) ⊕ π(jr) ⊕ π(kr) = br.

The Verifier has completeness (1-ε) and soundness 1/2 + ε (refer to PCP (complexity)). The Verifier satisfies

If the first of these two equations were equated to "=1" as usual, one could find a proof π by solving a system of linear equations (see MAX-3LIN-EQN) implying P = NP.

  • If z ∈ L, a fraction ≥ (1- ε) of clauses are satisfied.
  • If z ∉ L, then for a (1/2- ε) fraction of R, 1/4 clauses are contradicted.

This is enough to prove the hardness of approximation ratio

== Related problems ==

MAX-3SAT(B) is the restricted special case of MAX-3SAT where every variable occurs in at most B clauses. Before the PCP theorem was proven, Papadimitriou and Yannakakis[2] showed that for some fixed constant B, this problem is MAX SNP-hard. Consequently with the PCP theorem, it is also APX-hard. This is useful because MAX-3SAT(B) can often be used to obtain a PTAS-preserving reduction in a way that MAX-3SAT cannot. Proofs for explicit values of B include: all B ≥ 13,[3][4] and all B ≥ 3[5] (which is best possible).

Moreover, although the decision problem 2SAT is solvable in polynomial time, MAX-2SAT(3) is also APX-hard.[5]

The best possible approximation ratio for MAX-3SAT(B), as a function of B, is at least 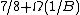and at most 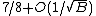,[6] unless NP=RP. Some explicit bounds on the approximability constants for certain values of B are known.[7]

[8][9] Berman, Karpinski and Scott proved that for the "critical" instances of MAX-3SAT in which each literal occurs exactly twice, and each clause is exactly of size 3, the problem is approximation hard for some constant factor.[10]

MAX-EkSAT is a parameterized version of MAX-3SAT where every clause has exactly literals, for k ≥ 3. It can be efficiently approximated with approximation ratio 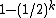using ideas from coding theory.

It has been proved that random instances of MAX-3SAT can be approximated to within factor 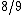.[11]

References

1. ^{{cite journal|last1=Håstad|first1=Johan|title=Some optimal inapproximability results|journal=Journal of the ACM|volume=48|issue=4|year=2001|page=798–859|doi=10.1145/502090.502098|citeseerx=10.1.1.638.2808}}
2. ^Christos Papadimitriou and Mihalis Yannakakis, Optimization, approximation, and complexity classes, Proceedings of the twentieth annual ACM symposium on Theory of computing, p.229-234, May 02–04, 1988.
3. ^Rudich et al., "Computational Complexity Theory," IAS/Park City Mathematics Series, 2004 page 108 {{ISBN|0-8218-2872-X}}
4. ^Sanjeev Arora, "Probabilistic Checking of Proofs and Hardness of Approximation Problems," Revised version of a dissertation submitted at CS Division, U C Berkeley, in August 1994. CS-TR-476-94. Section 7.2.
5. ^1 Ausiello, G., Crescenzi, P., Gambosi, G., Kann, V., Marchetti Spaccamela, A., and Protasi, M. (1999), Complexity and Approximation. Combinatorial Optimization Problems and their Approximability Properties, Springer-Verlag, Berlin. Section 8.4.
6. ^Luca Trevisan. 2001. Non-approximability results for optimization problems on bounded degree instances. In Proceedings of the thirty-third annual ACM symposium on Theory of computing (STOC '01). ACM, New York, NY, USA, 453-461. DOI=10.1145/380752.380839 http://doi.acm.org/10.1145/380752.380839
7. ^On some tighter inapproximability results, Piotr Berman and Marek Karpinski, Proc. ICALP 1999, pages 200--209.
8. ^P. Berman and M. Karpinski, Improved Approximation Lower Bounds on Small Occurrence Optimization, ECCC TR 03-008 (2003)
9. ^P. Berman, M. Karpinski and A. D. Scott, Approximation Hardness and Satisfiability of Bounded Occurrence Instances of SAT,ECCC TR 03-022 (2003).
10. ^P. Berman, M. Karpinski and A. D. Scott, Approximation Hardness of Short Symmetric Instances of MAX-3SAT,ECCC TR 03-049 (2003).
11. ^W.F.de la Vega and M.Karpinski, 9/8-Approximation Algorithm for Random MAX-3SAT,ECCC TR 02-070 (2002);RAIRO-Operations Research 41(2007),pp.95-107]
Lecture Notes from University of California, BerkeleyCoding theory notes at University at Buffalo

2 : Satisfiability problems|NP-hard problems
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/12 1:58:27