独立性检验dulixing jianyan

指以列联表形式出现的两种分类准则是否独立的假设检验。若否定假设，就认为两种分类准则之间存在关联性或相依性。列联表的记数形式见表1。

表1 K×C的列联表

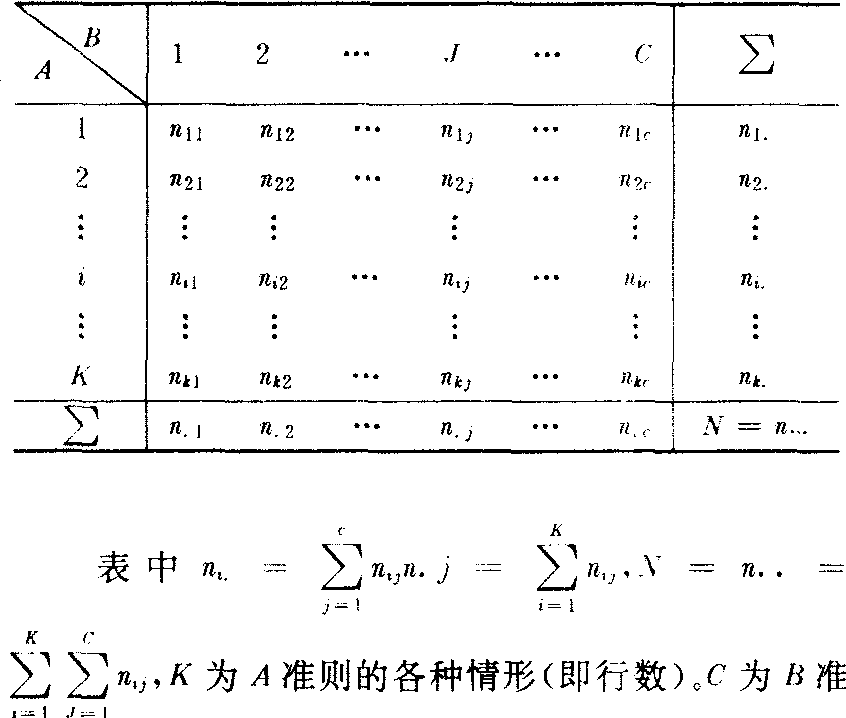
则的各种情形（即列数）。若A、B独立，则P(A_iB_j)=P(A_i)P(B_i)，而P(A_i)=＝n_i/N、P(B_j)=＝n_.j/N；实际观测次数为n_ij,相应的理论次数fe=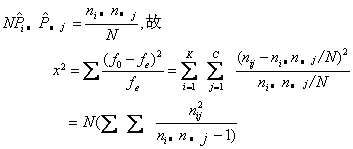
它服从于自由度为(K-1)(C-1)的X²分布。
[例] 调查家庭经济状况为上、中、下三类的高中毕业生150人，他们对于报考师范大学的态度亦有三种：愿意、不愿意、未定。其人数分布情况如下。问学生对报考师范大学的态度是否与家庭经济状况有关？

报考态度 经济状况	愿意	不愿意	未定	∑
上	18(20.9)	28(19.8)	10(15.3)	56
中	20(21.7)	18(20.5)	20(15.9)	58
下	18(13.4)	7(12.7)	11(9.8)	36
Σ	56	53	41	150

设H₀学生报考师范大学的态度与家庭经济状况独立（或无关）。若用前部分公式计X²值，则先计理论值f_e＝ni._n.j/N，并把结果写入表中括号内；若用后部分公式计（此法较为准确），则可直接代入公式：

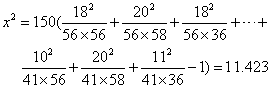
依f=(3-1)(3-1)=4及a=0.05查X²分布表得X(_4)0.052=9.49，因X²>X(4_)0.052,故拒绝H0，即学生报考师范大学的态度与家庭经济状况有关。
在表1中，当A、B均为二种可能性时，表1为2×2的列联表（见下表）。此时可用下式计X2值：

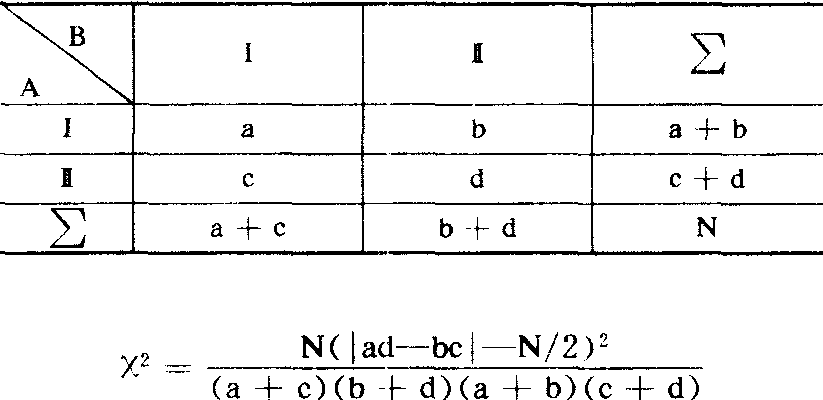
当检验结果为拒绝H⁰时，则可用下式计算这两种分类准则之间的关联程度

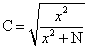
式中 X^2——所计得的值
N——总次数
C——列联系数
在上例中把X²＝11.423及N=150代入上式得：

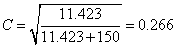
此处无需对C再作显著性检验。列联系数是两类准则关联程度的一种测度。