猫捕鼠Mao bu shu

1494年，意大利数学家帕乔利(Pacioli,L.，约1445—1517)出版了《算术、几何及比例性质摘要》， 书中收入了这样一个有趣的问题：“一只老鼠在60尺高的白杨树顶上，一只猫在树脚下的地上。老鼠每天下降半尺， 晚上又上升1/6尺，猫每天往上爬1尺，晚上又滑下1/4尺。这棵树在猫和老鼠之间那一段每天长1/4尺，晚上又缩短1/8。问猫要多久才能捉到老鼠。“注意到老鼠每昼夜实际下降了
由于二者之间最初的距离是60尺，先用除法求得天数的整数部分：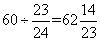
于是可知， 经过62昼夜， 猫鼠之间的距离缩短了：
天， 猫鼠之间距离可以缩短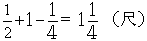
1522年，在德国数学家里斯(Riese,A.,1492—1559) 出版的一本算术书里给出了一个简单得多的问题，可以看作上 一题的原型：“井深20尺，蜗牛在井底，白天爬上7尺， 夜里降回2尺， 问几天后可以到达井顶。”立即可以看出，经过3昼夜，蜗牛上升了15尺，
把最后一天与前面各天所完成的距离区别开。在里斯的例子中，如果依据每天实际上升5尺、爬完20尺要用4天去计算， 就完全错误了。
类似的问题在文艺复兴时期曾出现在许多欧洲国家的数学书中，一个颇具实际背景的例子是在1559年法国数学家彪特(Buteo,J.，约1489—约1566)的一本算术书中给出的， 我们请读者去解答：
相距20 000视距尺的两只船起锚相向而行。第一只船天亮起航时遇到北风，快黄昏走了1 200视距尺，又起了西南风。此时另一只船起航，并且在夜间航行了1 400视距尺。第一只船由于顶风往回走了700视距尺。而早晨的北风， 使第一只船像平常出航那样向前走，另一只船则往回走600视距尺。黑夜和白天如此交替，遇到顺风往前行，遇到顶风往回走。试问：两只船在相遇之前， 一共航行了多少路？