“Partial equivalence relation”的意思、由来-开放百科全书

In mathematics, a partial equivalence relation (often abbreviated as PER, in older literature also called restricted equivalence relation)

on a set

is a relation that is symmetric and transitive. In other words, it holds for all

that:

Properties and applications

In a set-theoretic context, there is a simple structure to the general PER

: it is an equivalence relation on the subset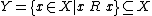

. (

is the subset of

such that in the complement of

(

) no element is related by

to any other.) By construction,

is reflexive on

and therefore an equivalence relation on

. Notice that

is actually only true on elements of

: if

, then

by symmetry, so

and

by transitivity. Conversely, given a subset Y of X, any equivalence relation on Y is automatically a PER on X. Hence, in set theory one typically studies the equivalence relation associated with a PER, rather than the PER itself.

But in type theory, constructive mathematics and their applications to computer science, constructing analogues of subsets is often problematic^[1]—in these contexts PERs are therefore more commonly used, particularly to define setoids, sometimes called partial setoids. Forming a partial setoid from a type and a PER is analogous to forming subsets and quotients in classical set-theoretic mathematics.

Every partial equivalence relation is a difunctional relation, but the converse does not hold.

The algebraic notion of congruence can also be generalized to partial equivalences, yielding the notion of subcongruence, i.e. a homomorphic relation that is symmetric and transitive, but not necessarily reflexive.^[2]

Examples

A simple example of a PER that is not an equivalence relation is the empty relation

(unless

, in which case the empty relation is an equivalence relation (and is the only relation on

)).

Kernels of partial functions

For another example of a PER, consider a set

and a partial function

that is defined on some elements of

but not all. Then the relation

defined by

is a partial equivalence relation but not an equivalence relation. It possesses the symmetry and transitivity properties, but it is not reflexive since if

is not defined then

— in fact, for such an

there is no

such that

. (It follows immediately that the subset of

for which

is an equivalence relation is precisely the subset on which

is defined.)

Functions respecting equivalence relations

Let X and Y be sets equipped with equivalence relations (or PERs)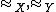

. For

, define

to mean:

then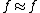

means that f induces a well-defined function of the quotients

. Thus, the PER

captures both the idea of definedness on the quotients and of two functions inducing the same function on the quotient.

Equality of IEEE floating point values

IEEE 754:2008 floating point standard defines an "EQ" relation for floating point values. This predicate is symmetrical and transitive, but is not reflexive because of the presence of [NaN] values that are not EQ to themselves.

References