032 盈不足术
即今算术中解盈亏类问题的方法。为中国古算的一个创造。《九章算术》辟专章阐述。分盈不足、两盈、两不足、盈与适足、不足与适足诸情况给出解法。《九章算术》盈不足章中给出8个盈亏类问题。另有12个非盈亏类问题仍用盈不足术求解。其方法是：先任意假设答数然后再验算。结果无非是相符(即假设的答数正确)或不符。若不符，再假设一次，其结果或盈不足，或两盈，或两不足，或一盈一适足，或一不足一适足。从而将非盈亏类问题化为盈亏类问题，用盈不足术解之。西方称此法为“契丹(阿拉伯和西方对中国的称呼)算法”、“双设法”、“双假位法”、“金法”。直到17世纪，盈不足术仍是欧洲解决各类算术问题的主要方法。盈不足术实际上就是现代的线性插值法(截弦法)。在解高次代数方程和超越方程中还常常用到。
盈不足术Yingbuzushu
在中国古代，为了求解各种复杂多样的线性问题与非线性问题， 创造了一种独具特色的数学方法——盈不足术。这种方法，通过两次假设及检验， 把复杂的数学问题转化为今天所说的盈亏类问题，用统一的模式给出解答。《九章算术》中专门设有“盈不足”一章，足见它在中国古代数学中的地位。
在盈不足术中，把假设数据称为“假令”，而把用“假令”进行检验考核的过程称为“课”，其结果不外乎“盈”、“不足”、“适足”三种情形、通过两次假设与考核， 其结果可分为 “盈不足”、“两盈” 或 “两不足”、“盈、适足”或“不足、适足”五种三类， 盈不足章的前8题就是以“共买物”问题为模型，给出了各类盈亏问题求解的演算法则，其第1题为：“今有共买物， 人出八，盈三：人出七，不足四。问人数、物价各几何。”一般说来，设每人出a1钱，盈b1; 每人出a2钱，不足b2，求人数A和物价B。若以x0表示每人应出的钱数，书中给出 “盈不足”类型问题求解的三条公式：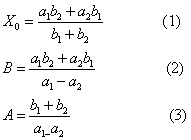
在第1题中， 由公式(2)、(3) 可得人数A=7，物价B=53。
两盈、两不足类问题的一般形式为：今有共买物，人出a1钱， 盈 （或不足）b1, 人出a2钱， 盈 （或不足）b2。问人数、物价各几何。书中相应地给出了三条公式：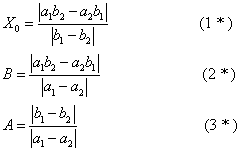
原文并不涉及正负数或绝对值概念， 但公式中凡遇二数之差一律取正数 （或非负数）。
盈（不足）、适足类问题一般形式为：今有共买物，人出a1钱，盈（不足）b1；人出a2钱，适足。问人数、物价各几何。书中给出的三条公式为：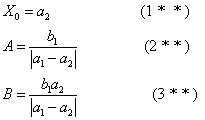
借助正负数概念， 上面的三组公式可以十分容易地统一起来。
盈不足术是中国数学史上的一项杰出成就， 在当时，人们不仅用它解决各种盈亏类问题，而且用以解决了一些复杂得多的问题 (参见 “良驽相逢”、“两鼠对穿”)，成为古代数学中的万能算法，其数学原理相当于今天数学中的线性插值法或弦位法。
在9—12世纪一些阿拉伯数学家的著作中， 曾介绍过盈不足术，并称之为天秤术或契丹算法。当时阿拉伯人所说的“契丹”就是中国。其后，盈不足术又经过阿拉伯传入欧洲。1202年，意大利数学家斐波那契在他的名著《算书》设有专门的一章介绍“契丹算法”，并写道： “契丹法， 阿拉伯名词； 拉丁译文当为迭借法，……又可称为增损术。”在中世纪的欧洲，盈不足术做为解决各种复杂问题的 一种万能算法， 曾受到极大的重视。直到16世纪仍以契丹法、迭借法、增损术之名广泛出现于各种数学书中， 在德国数学家克拉维斯(Clavius,C.1537- 1612)出版于1608年的一部代数书中，载有这样 一个问题“如果我给每一个上门的乞丐7分钱，还剩24分；要是给他们每人9分钱，就还差32分钱。试问： 有多少乞丐？ 我有多少钱？”
盈不足术
中国古代解决盈亏类问题的一种算术方法。在《九章算术》中有“盈不足”一章，其中前4个问题是正规的盈亏类问题，第5～8题依次是“两盈”问题，“两不足”问题，“盈、适足”及“不足、适足”问题。此外还有12个形式上不属于盈亏类，但都用盈不足术解答的算术问题。第1个，也是典型的问题是：“今有（人）共买物，（每）人出八（钱）盈（余）三（钱）;（每）人出七（钱）不足四（钱），问人数、物价各几何”。此题写成代数形式为：设每人出（钱）a1，盈b1，每人出a2，不足b2，求物价u和人数v。依所述方法可得u=(a2b1+a1b2)/(a1-a2),v=(b1+b2)/(a1-a2)。