直线和普遍二次曲面的相关位置zhixian he pubian erciqumian de xiangguan weizhi
设二次曲面
F (x,y,z) ≡φ (x,y,z) +
2ux+2vy+2wz+d= 0 (1)
φ (x,y,z) ≡ax2+by2+cz2+2fyz+ 2gzx+ 2hxy.l是过P0 (x0,y0,z0)方向余弦为λ,μ,γ的直线x =x0 +λt,y =y0 +μt,z = z0 +γt, (2)
将 (2)代入 (1),得t的二次方程Qy2+2Rt+S=0 (3)
Q=φ (λ,μ,γ)
R=λ(αx0+hy0+gz0+u)+μ (hx0+by0+fz0+v)+
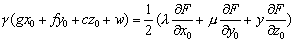
S=F (x0,y0,z0).
当Q≠0时,若R2-QS>0,则 (2)与 (1)有两个不同的交点,(2)叫做(1)的割线;若R2-QS=0,则 (2)与 (1)有一个交点 (看作两个点的重合),(2) 叫做 (1) 的切线; 若R2-QS<0,则 (2) 与(1) 无交点,(2) 叫做 (1) 的离线.
当Q=0,R≠0时,(3)的一个根趋于无穷,(2)叫做 (1) 的一个交点趋于无穷的割线.
当Q=R=0,S≠0时,(3)的两根趋于无穷,(2)叫做 (1) 的渐近线.
当Q=R=S=0时,t的任何值都适合方程(3),直线 (2) 完全在曲面 (1) 上,故 (2) 叫做 (1) 的母线.
注意: 曲面F (x,y,z) = 0上的一点 (x0,y0

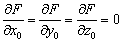 时,此点叫做奇异点,在奇异点处R= 0.
时,此点叫做奇异点,在奇异点处R= 0.