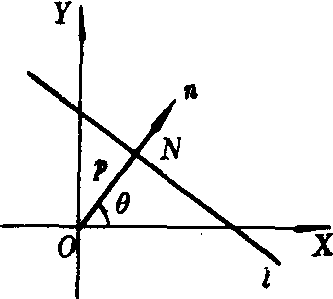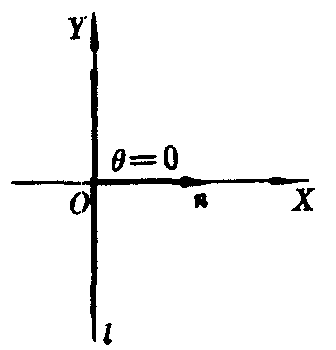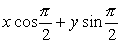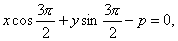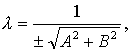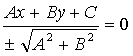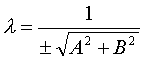直线方程的法线式zhixian fangcheng de faxianshi

若已知直线l，原点到直线l的距离为p(p≥0)，法线的方向角为θ(0≤θ<2π)，则直线l的方程xcosθ+ysinθ-p=0，叫做直线方程的法线式，或直线的法线式方程.
法线方向角θ规定如下：设直线l不经过原点，从原点引射线n垂直于直线l，交l于N点，这条射线叫做直线l的法线.(如图1)，线段ON的长|ON|用p表示(p>0)；从X轴的正方向到法线的正方向(从O到N的方向)所成的角叫做法线的方向角，用θ表示，(0≤θ<2π).

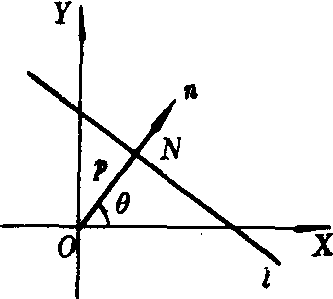
图1

当直线l经过原点时，规定法线的正方向向上，当直线l和Y轴重合时，规定法线正方向向右，这时0≤θ<π,p=0 (如图2).

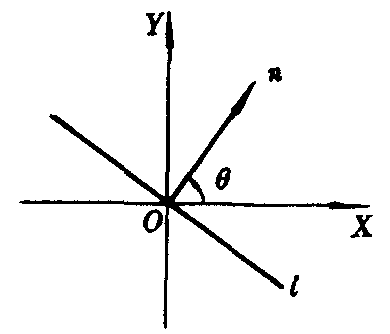
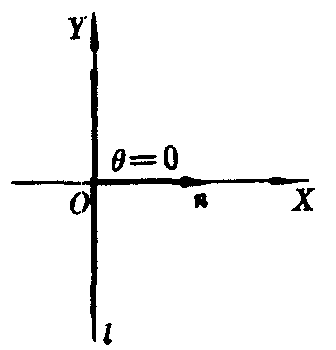
图2

根据上述规定，对于直角坐标平面内任意一条直线l都可以唯一确定一个有序实数对(p,θ)(其中p≥0)；反之，对于每一个有序实数对(p,θ) (其中p≥0)都可以唯一确定直角坐标平面内一条直线.
直线的法线式方程也能适用于过坐标原点或垂直于坐标轴的直线：当直线过原点时，p=0它的法线式方程是xcosθ+ysinθ=0；当直线平行于Y轴.且和Y轴距离为p时，θ=0或θ=π.它的法线式方程是xcos0+ysin0-p=0，即x-p=0或xcosπ+ysinπ-p=0，即-x-p=0；当直线平行于X轴，且和X轴距离为p时，θ

=π/2

或

θ=3π/2

它的法线式方程是

-p=0,

即

y-p＝0,

或

，即

-y

-p=0.

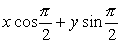
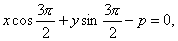
由此可知，直线的法线式方程可以表示平面内任何一条直线；反之，在平面直角坐标系中，任何一条直线都可用法线式方程表示.
直线方程的一般式化法线式的过程如下：
将方程Ax+By+C=0两端同乘以常数λ，得λAx+λBy+λC=0，由法线式的特点可得(λA)²+(λB)²＝

1, 且λC≤0, 因此

所得法线式方程

是

式中

叫做法线化因子， 或法化因子.

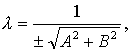
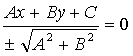
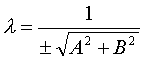
λ的符号确定应符合以下规定：当C≠0时，λ和C异号；当C=0.B≠0时，λ和B同号；当C=0,B=0 (这时A≠0),λ和A同号.
利用直线l的法线式方程xcosθ+ysinθ-p=0，可以很快求出原点到直线l的距离就是p，由此可以进一步导出平面上任意一点P₁ (x₁,y₁)到直线l:xcosθ+ysinθ-p=0的距离d=|x₁cosθ+y₁sinθ-p|.