相遇问题Xiangyu wenti

内容广泛，形式多样的行程问题，是小学数学应用题中的难点之一，而它们在中国古代的《九章算术》及《张邱建算经》中早已有着丰富的类型与完整的解法， 在较晚的外国数学著作中也有不少类似的问题。这里我们集中介绍古代的相遇问题， 而对追及问题则另行介绍。
《九章算术》均输章第20题： “今有凫(注：野鸭子)起南海，七日至北海； 雁起北海，九日至南海。今凫雁俱起， 问何日相逢。”根据原书的解题过程， 可知凫雁相逢所需的时间为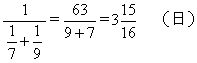
均输章第21题：“今有甲发(注：出发)长安，五日至齐；乙发齐，七日至长安。今乙发已先二日，甲乃发长安。问几何(注： 多少) 日相逢。”甲、乙每日路
逢所需的时间为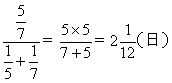
在6世纪初印度数学家阿利哈塔的 一本关于天文学和数学的小册子中，有关于两星相遇的问题： “相距为d的两颗星，分别以速度V₁和V₂相向运动，求两星相遇的地点。”书中给出相遇地点到第一颗星的初始
另一方面， 由于相遇问题所涉及的是相向而行的双方共同走过的距离， 因而又可归入讨论同工共作的“工程问题”，实际上，在《九章算术》中这两类问题就是用相同的方法解决的。