- Statement of Theorem
- References
In mathematics, particularly in the field of differential topology, the preimage theorem is a variation of the implicit function theorem concerning the preimage of particular points in a manifold under the action of a smooth map.[1][2]
Statement of Theorem
Definition. Let  be a smooth map between manifolds. We say that a point
be a smooth map between manifolds. We say that a point 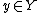 is a regular value of f if for all
is a regular value of f if for all 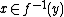 the map
the map  is surjective. Here,
is surjective. Here, 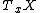 and
and  are the tangent spaces of X and Y at the points x and y.
are the tangent spaces of X and Y at the points x and y.
Theorem. Let  be a smooth map, and let
be a smooth map, and let 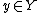 be a regular value of f; then
be a regular value of f; then 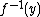 is a submanifold of X. If
is a submanifold of X. If 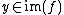 , then the codimension of
, then the codimension of 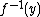 is equal to the dimension of Y. Also, the tangent space of
is equal to the dimension of Y. Also, the tangent space of 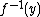 at
at  is equal to
is equal to 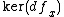 .
.
References
1. ^{{citation|title=An Introduction to Manifolds|first=Loring W.|last=Tu|publisher=Springer|year=2010|isbn=9781441974006|contribution=9.3 The Regular Level Set Theorem|pages=105–106|url=https://books.google.com/books?id=xQsTJJGsgs4C&pg=PA105}}.
2. ^{{citation|title=Lectures on Morse Homology|volume=29|series=Texts in the Mathematical Sciences|first=Augustin|last=Banyaga|publisher=Springer|year=2004|isbn=9781402026959|page=130|url=https://books.google.com/books?id=AX-_sbMjOK4C&pg=PA130|contribution=Corollary 5.9 (The Preimage Theorem)}}.
{{topology-stub}}2. ^{{citation|title=Lectures on Morse Homology|volume=29|series=Texts in the Mathematical Sciences|first=Augustin|last=Banyaga|publisher=Springer|year=2004|isbn=9781402026959|page=130|url=https://books.google.com/books?id=AX-_sbMjOK4C&pg=PA130|contribution=Corollary 5.9 (The Preimage Theorem)}}.
1 : Theorems in differential topology
- Laibach
- Laibach (album)
- Laibach (disambiguation)
- Lai Changxing
- Lai-Chau
- Lai Chi Kok
- Lai Chi Kok station
- Lai Chi Ying
- Lai Châu
- Laicism
- Laicite
- Laicity
- Laicité
- Laid (album)
- Laid Back
- Laidlaw
- Laidlaw, British Columbia
- Laidlaw International, Inc
- Laid Off
- La'ie
- Laie
- Laie, Hawaii
- Laie Hawaii Temple
- Laie, HI
- L'Aigle