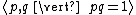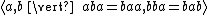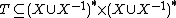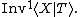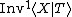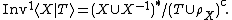“Presentation of a monoid”的意思、由来-开放百科全书

词条

Presentation of a monoid

释义

Construction
Inverse monoids and semigroups
Notes
References

In algebra, a presentation of a monoid (respectively, a presentation of a semigroup) is a description of a monoid (respectively, a semigroup) in terms of a set {{math|Σ}} of generators and a set of relations on the free monoid {{math|Σ^∗}} (respectively, the free semigroup {{math|Σ⁺}}) generated by {{math|Σ}}. The monoid is then presented as the quotient of the free monoid (respectively, the free semigroup) by these relations. This is an analogue of a group presentation in group theory.

As a mathematical structure, a monoid presentation is identical to a string rewriting system (also known as a semi-Thue system). Every monoid may be presented by a semi-Thue system (possibly over an infinite alphabet).^[1]

A presentation should not be confused with a representation.

Construction

The relations are given as a (finite) binary relation {{mvar|R}} on {{math|Σ^∗}}. To form the quotient monoid, these relations are extended to monoid congruences as follows:

First, one takes the symmetric closure {{math|R ∪ R⁻¹}} of {{mvar|R}}. This is then extended to a symmetric relation {{math|E ⊂ Σ^∗ × Σ^∗}} by defining {{math|x ~_E y}} if and only if {{mvar|x}} = {{mvar|sut}} and {{mvar|y}} = {{mvar|svt}} for some strings {{math|u, v, s, t ∈ Σ^∗}} with {{math|(u,v) ∈ R ∪ R⁻¹}}. Finally, one takes the reflexive and transitive closure of {{mvar|E}}, which then is a monoid congruence.

In the typical situation, the relation {{mvar|R}} is simply given as a set of equations, so that 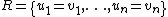. Thus, for example,

is the equational presentation for the bicyclic monoid, and

is the plactic monoid of degree 2 (it has infinite order). Elements of this plactic monoid may be written as 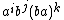for integers i, j, k, as the relations show that ba commutes with both a and b.

Inverse monoids and semigroups

Presentations of inverse monoids and semigroups can be defined in a similar way using a pair

where

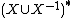
is the free monoid with involution on , and

is a binary relation between words. We denote by 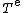(respectively 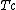) the equivalence relation (respectively, the congruence) generated by T.

We use this pair of objects to define an inverse monoid

Let 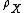be the Wagner congruence on , we define the inverse monoid

presented by 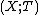as

In the previous discussion, if we replace everywhere 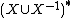with 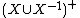we obtain a presentation (for an inverse semigroup) 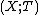and an inverse semigroup 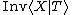presented by .

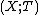A trivial but important example is the free inverse monoid (or free inverse semigroup) on , that is usually denoted by 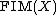(respectively 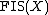) and is defined by

Notes

1. ^Book and Otto, Theorem 7.1.7, p. 149

References

John M. Howie, Fundamentals of Semigroup Theory (1995), Clarendon Press, Oxford {{ISBN|0-19-851194-9}}
M. Kilp, U. Knauer, A.V. Mikhalev, Monoids, Acts and Categories with Applications to Wreath Products and Graphs, De Gruyter Expositions in Mathematics vol. 29, Walter de Gruyter, 2000, {{ISBN|3-11-015248-7}}.
Ronald V. Book and Friedrich Otto, String-rewriting Systems, Springer, 1993, {{ISBN|0-387-97965-4}}, chapter 7, "Algebraic Properties"

1 : Semigroup theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。