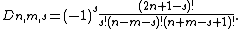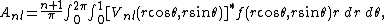“Pseudo-Zernike polynomials”的意思、由来-开放百科全书

词条

Pseudo-Zernike polynomials

释义

Definition
Examples
Moments
See also
References

In mathematics, pseudo-Zernike polynomials are well known and widely used in the analysis of optical systems. They are also widely used in image analysis as shape descriptors.

Definition

They are an orthogonal set of complex-valued polynomials

defined as

where 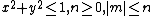and orthogonality on the unit disk is given as

where the star means complex conjugation, and

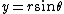
are the standard transformations between polar and Cartesian coordinates.

The radial polynomials 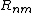are defined as^[1]

with integer coefficients

Examples

Examples are:

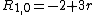
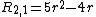
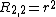
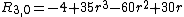
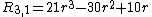
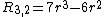
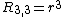
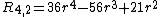
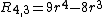
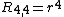
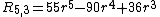
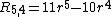
Moments

The pseudo-Zernike Moments (PZM) of order and repetition are defined as

where , and takes on positive and negative integer

values subject to .

The image function can be reconstructed by expansion of the pseudo-Zernike coefficients on the unit disk as

Pseudo-Zernike moments are derived from conventional Zernike moments and shown

to be more robust and less sensitive to image noise than the Zernike moments.^[1]

References

1. ^¹{{cite journal|first1=C.-H.|last1=Teh|last2=Chin|first2=R.|title=On image analysis by the methods of moments|journal=IEEE Transactions on Pattern Analysis and Machine Intelligence|volume=10|issue=4|year=1988|pages=496–513|doi=10.1109/34.3913}}

{{cite journal

|last1=Belkasim
|first1=S.
|last2=Ahmadi
|first2=M.
|last3=Shridhar
|first3=M.
|title=Efficient algorithm for the fast computation of zernike moments
|journal=Journal of the Franklin Institute
|year=1996
|volume=333
|issue=4
|pages=577–581
|doi=10.1016/0016-0032(96)00017-8
}}

{{cite journal

|last1=Haddadnia
|first1=J.
|last2=Ahmadi
|first2=M.
|last3=Faez
|first3=K.
|title=An efficient feature extraction method with pseudo-zernike moment in rbf neural network-based human face recognition system
|journal=EURASIP Journal on Applied Signal Processing
|year=2003
|pages=890–901
|doi=10.1155/S1110865703305128
|volume=2003
|issue=9
}}

{{cite conference

|author= T.-W. Lin
|author2=Y.-F. Chou
|title=A comparative study of zernike moments
|conference=Proceedings of the IEEE/WIC International Conference on Web Intelligence
|year=2003
|pages=516–519
|url=http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=1241255
|isbn=0-7695-1932-6
}}

{{ cite journal

|first1=C.-W.
|last1=Chong
|first2=P.
|last2=Raveendran
|first3=R.
|last3=Mukundan
|title=The scale invariants of pseudo-Zernike moments
|journal=Pattern Anal. Applic.
|year=2003
|volume=6
|pages=176–184
|doi=10.1007/s10044-002-0183-5
|issue=3
}}

{{cite journal

|journal=Int. J. Pattern Recogn. Artif. Int.
|year=2003
|volume=17
|issue=6
|pages=1011–1023
|doi= 10.1142/S0218001403002769
|url=http://ir.canterbury.ac.nz/bitstream/10092/448/1/12584534_ivcnz01.pdf
|first1=Chee-Way
|last1=Chong
|first2=R.
|last2=Mukundan
|first3=P.
|last3=Raveendran
|title=An Efficient Algorithm for Fast Computation of Pseudo-Zernike Moments
}}

{{cite web

|first1=Jamie
|last1=Shutler
|url=http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/SHUTLER3/node11.html |title=Complex Zernike Moments
|year=1992
}}{{DEFAULTSORT:Pseudo-Zernike Polynomials}}

1 : Orthogonal polynomials

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Definition

Examples

Moments

See also

References