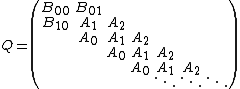“Quasi-birth–death process”的意思、由来-开放百科全书

In queueing models, a discipline within the mathematical theory of probability, the quasi-birth–death process describes a generalisation of the birth–death process.^[1]^[2]{{rp|118}} As with the birth-death process it moves up and down between levels one at a time, but the time between these transitions can have a more complicated distribution encoded in the blocks.

Discrete time

where each of A₀, A₁ and A₂ are matrices and A*₀, A*₁ and A*₂ are irregular matrices for the first and second levels.^[4]

Continuous time

The transition rate matrix for a quasi-birth-death process has a tridiagonal block structure

where each of B₀₀, B₀₁, B₁₀, A₀, A₁ and A₂ are matrices.^[5] The process can be viewed as a two dimensional chain where the block structure are called levels and the intra-block structure phases.^[6] When describing the process by both level and phase it is a continuous-time Markov chain, but when considering levels only it is a semi-Markov process (as transition times are then not exponentially distributed).

Usually the blocks have finitely many phases, but models like the Jackson network can be considered as quasi-birth-death processes with infinitely (but countably) many phases.^[6]^[7]

Stationary distribution

The stationary distribution of a quasi-birth-death process can be computed using the matrix geometric method.

References

1. ^{{Cite book | last1 = Latouche | first1 = G. | chapter = Level-Independent Quasi-Birth-and-Death Processes | doi = 10.1002/9780470400531.eorms0461 | title = Wiley Encyclopedia of Operations Research and Management Science | year = 2011 | isbn = 9780470400531 | pmid = | pmc = }}
2. ^{{cite book | first = Natarajan | last = Gautam | title = Analysis of Queues: Methods and Applications | publisher = CRC Press | year = 2012 | isbn = 9781439806586}}
3. ^{{Cite journal | last1 = Latouche | first1 = G. | last2 = Pearce | first2 = C. E. M. | last3 = Taylor | first3 = P. G. | title = Invariant measures for quasi-birth-and-death processes | doi = 10.1080/15326349808807481 | journal = Communications in Statistics. Stochastic Models | volume = 14 | pages = 443 | year = 1998 | pmid = | pmc = }}
4. ^{{Cite book | last1 = Palugya | first1 = S. N. | last2 = Csorba | first2 = M. T. J. | chapter = Modeling Access Control Lists with Discrete-Time Quasi Birth-Death Processes | doi = 10.1007/11569596_26 | title = Computer and Information Sciences - ISCIS 2005 | series = Lecture Notes in Computer Science | volume = 3733 | pages = 234 | year = 2005 | isbn = 978-3-540-29414-6 | pmid = | pmc = }}
5. ^{{Cite book | first1=S. R. |last1=Asmussen| doi = 10.1007/0-387-21525-5_11 | chapter = Markov Additive Models | title = Applied Probability and Queues | series = Stochastic Modelling and Applied Probability | volume = 51 | pages = 302–339 | year = 2003 | isbn = 978-0-387-00211-8 | pmid = | pmc = }}
6. ^¹{{Cite journal | last1 = Kroese | first1 = D. P. | last2 = Scheinhardt | first2 = W. R. W. | last3 = Taylor | first3 = P. G. | doi = 10.1214/105051604000000477 | title = Spectral properties of the tandem Jackson network, seen as a quasi-birth-and-death process | journal = The Annals of Applied Probability | volume = 14 | issue = 4 | pages = 2057 | year = 2004 | pmid = | pmc = | arxiv = math/0503555 }}
7. ^{{Cite journal | last1 = Motyer | first1 = A. J. | last2 = Taylor | first2 = P. G. | doi = 10.1239/aap/1151337083 | title = Decay rates for quasi-birth-and-death processes with countably many phases and tridiagonal block generators | journal = Advances in Applied Probability | volume = 38 | issue = 2 | pages = 522 | year = 2006 | pmid = | pmc = }}