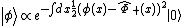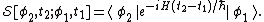“Schrödinger functional”的意思、由来-开放百科全书

词条

Schrödinger functional

释义

Example: Scalar Field
References

In mathematical physics, some approaches to quantum field theory are more popular than others. For historical reasons, the Schrödinger representation is less favoured than Fock space methods. In the early days of quantum field theory, maintaining symmetries such as Lorentz invariance, displaying them manifestly, and proving renormalisation were of paramount importance. The Schrödinger representation is not manifestly Lorentz invariant and its renormalisability was only shown as recently as the 1980s by Kurt Symanzik (1981).

Within the Schrödinger representation, the Schrödinger wavefunctional stands out as perhaps the most useful and versatile functional tool, though interest in it is specialized at present.

The Schrödinger functional is, in its most basic form, the time translation generator of state wavefunctionals. In layman's terms, it defines how a system of quantum particles evolves through time and what the subsequent systems look like.

Example: Scalar Field

In the quantum field theory of (as example) a quantum scalar field , in complete analogy with the one-particle quantum harmonic oscillator, the eigenstate of this quantum field with the "classical field" 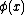(c-number) as its eigenvalue,

is (Schwartz, 2013)

where is the part of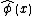

that only includes creation operators . For the oscillator, this corresponds to the representation change/map to the |x⟩ state from Fock states.

For a time-independent Hamiltonian {{mvar|H}}, the Schrödinger functional is defined as

In the Schrödinger representation, this functional generates time translations of state wave functionals, through

.

References

Brian Hatfield, Quantum Field Theory of Point Particles and Strings. Addison Wesley Longman, 1992. See Chapter 10 "Free Fields in the Schrodinger Representation".
I.V. Kanatchikov, "Precanonical Quantization and the Schroedinger Wave Functional." Phys. Lett. A 283 (2001) 25–36. Eprint [https://arxiv.org/abs/hep-th/0012084 arXiv:hep-th/0012084], 16 pages.
R. Jackiw, "Schrodinger Picture for Boson and Fermion Quantum Field Theories." In Mathematical Quantum Field Theory and Related Topics: Proceedings of the 1987 Montréal Conference Held September 1–5, 1987 (eds. J.S. Feldman and L.M. Rosen, American Mathematical Society 1988).
H. Reinhardt, C. Feuchter, "On the Yang-Mills wave functional in Coulomb gauge." Phys. Rev. D 71 (2005) 105002. Eprint [https://arxiv.org/abs/hep-th/0408237 arXiv:hep-th/0408237], 9 pages.
D.V. Long, G.M. Shore, "The Schrodinger Wave Functional and Vacuum States in Curved Spacetime." Nucl.Phys. B 530 (1998) 247–278. Eprint [https://arxiv.org/abs/hep-th/9605004 arXiv:hep-th/9605004], 41 pages.
Kurt Symanzik, "Schrödinger representation and Casimir effect in renormalizable quantum field theory". Nucl. Phys.B 190 (1981) 1–44, [https://dx.doi.org/10.1016/0550-3213(81)90482-X doi:10.1016/0550-3213(81)90482-X].
K. Symanzik, "Schrödinger Representation in Renormalizable Quantum Field Theory". Chapter in Structural Elements in Particle Physics and Statistical Mechanics, NATO Advanced Study Institutes Series 82 (1983) pp 287–299, [https://dx.doi.org/10.1007/978-1-4613-3509-2_20 doi:10.1007/978-1-4613-3509-2_20].
Martin Lüscher, Rajamani Narayanan, Peter Weisz, Ulli Wolff, "The Schrödinger Functional - a Renormalizable Probe for Non-Abelian Gauge Theories". Nucl.Phys.B 384 (1992) 168-228, [https://dx.doi.org/10.1016/0550-3213(92)90466-O doi:10.1016/0550-3213(92)90466-O]. Eprint [https://arxiv.org/abs/hep-lat/9207009 arXiv:hep-lat/9207009].
Matthew Schwartz (2013). Quantum Field Theory and the Standard Model, Cambridge University Press, Ch.14.

2 : Quantum field theory|Erwin Schrödinger

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。