统计假设检验statistical hypothesis test

对所研究的未知或部分未知总体提出一些假设，由样本的实际结果经过一定计算作出概率意义上应当接受何种假设的检验。
例如某小麦品种的平均千粒重μ0=36克，标准差σ=0.9克，若在小麦生育后期用KH₂PO₄进行根外追肥，成熟后测得10个样品的平均千粒重＝37.9克，那么-μ₀＝1.9克是根外追肥的效果还是随机抽样误差？统计假设检验可以对此作出回答。其具体步骤如下：❶提出无效假设H₀，即实得差异(与μ0之差)由误差造成的；备择假设HA，即实得差异由总体参数不同所致，它与H₀相对立。
❷选取统计量，明确其分布。
❸确定显著性水平α，即否定H0的概率水准。农化研究中α常取0.05或0.01。
❹在H0为正确的假设下，由统计量的抽样分布算出实得差异属于随机误差的概率p。
❺根据“小概率的实际不可能性原理”，当P≤α时则在α水平上否定H₀接受HA，推断实得差异由总体参数不同所致；若P≥α则接受H₀否定HA，推断实得差异属于随机误差。
接受区间和否定区间 根据显著性水平α将统计量的分布划分为接受H₀的区间和否定H₀的区间，分别简称为接受区间与否定区间。当样本统计量落在接受区间内则接受H₀否定H_A。反之，则否定H₀接受H_A。如标准正态变量u的分布中p(-1.96≤u≤1.96)=0.95，而P(u<-1.96或u>1.96)=0.05，所以当α取0.05时，u分布的接受区间为(-1.96,1.96)；否定区间为(-∞,-1.96)或(1.96,∞)。
统计假设检验的两类错误 当H₀客观上是真实的，但通过假设试验却否定了它，就犯了否定真实假设的错误，称为第一类错误，其概率为α。当H₀客观上是不正确的，但经假设检验却接受了它，则犯了接受不真实H₀的错误，称为第二类错误，其概率为β。
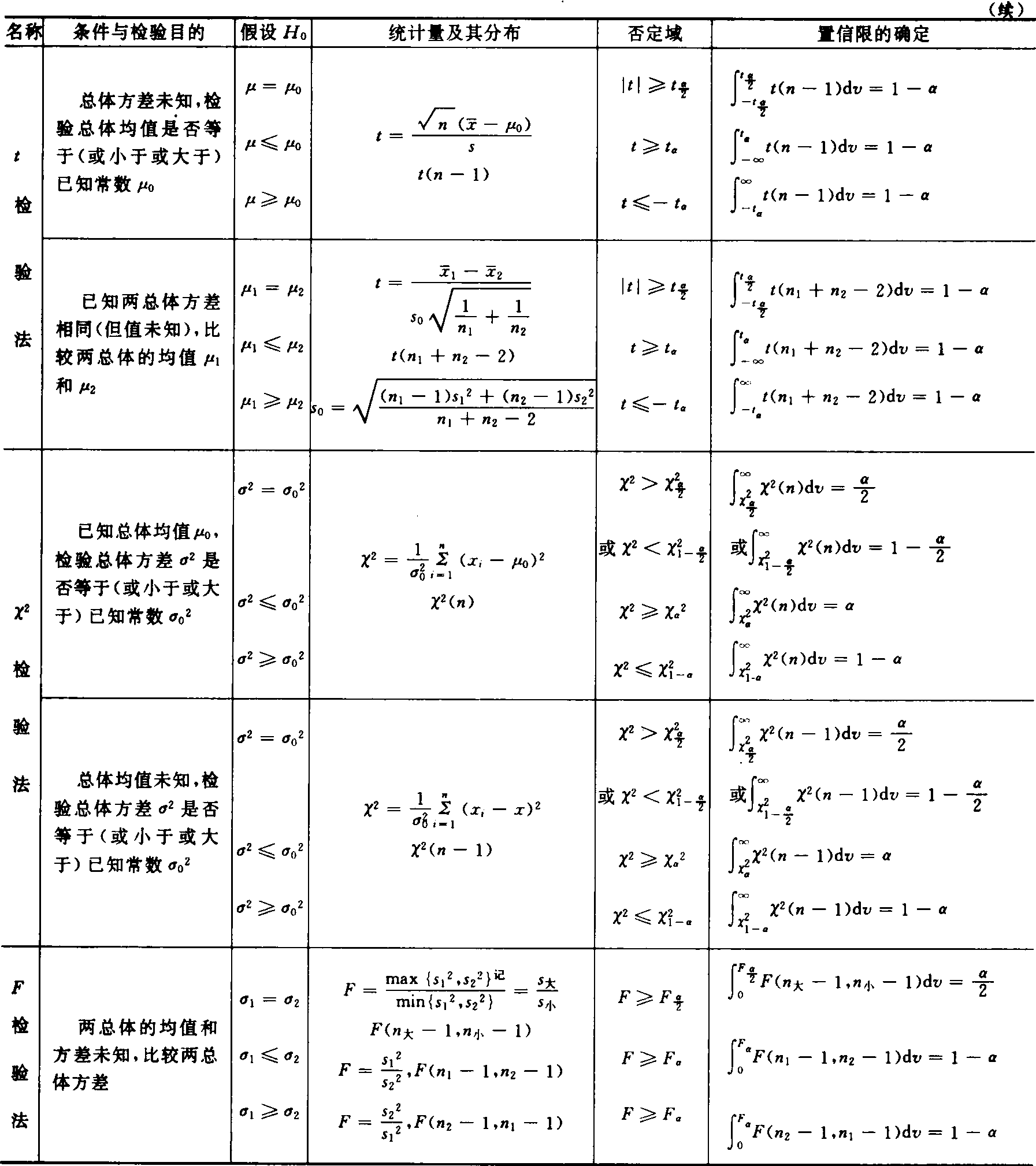
正态总体参数的统计假设检验表 农业化学研究中的许多随机变量服从正态分布，它们的平均数μ和方差σ²的检验因已知条件不同须分别采用u检验、t检验、x²检验和F检验如表所示。

正态总体参数的统计检验表