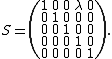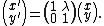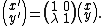“Shear matrix”的意思、由来-开放百科全书

词条

Shear matrix

释义

Properties
Applications
See also
Notes
References

In mathematics, a shear matrix or transvection is an elementary matrix that represents the addition of a multiple of one row or column to another. Such a matrix may be derived by taking the identity matrix and replacing one of the zero elements with a non-zero value.

A typical shear matrix is shown below:

The name shear reflects the fact that the matrix represents a shear transformation. Geometrically, such a transformation takes pairs of points in a linear space, that are purely axially separated along the axis whose row in the matrix contains the shear element, and effectively replaces those pairs by pairs whose separation is no longer purely axial but has two vector components. Thus, the shear axis is always an eigenvector of S.

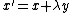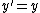A shear parallel to the x axis results in and . In matrix form:

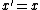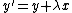Similarly, a shear parallel to the y axis has and . In matrix form:

Clearly the determinant will always be 1, as no matter where the shear element is placed, it will be a member of a skew-diagonal that also contains zero elements (as all skew-diagonals have length at least two) hence its product will remain zero and won't contribute to the determinant. Thus every shear matrix has an inverse, and the inverse is simply a shear matrix with the shear element negated, representing a shear transformation in the opposite direction. In fact, this is part of an easily derived more general result: if S is a shear matrix with shear element , then Sⁿ is a shear matrix whose shear element is simply n. Hence, raising a shear matrix to a power n multiplies its shear factor by n.

Properties

If S is an n×n shear matrix, then:

S has rank n and therefore is invertible
1 is the only eigenvalue of S, so det S = 1 and trace S = n
the eigenspace of S has n-1 dimensions.
S is asymmetric
S may be made into a block matrix by at most 1 column interchange and 1 row interchange operation
the area, volume, or any higher order interior capacity of a polytope is invariant under the shear transformation of the polytope's vertices.

Applications

Shear matrices are often used in computer graphics.^[1]

Notes

1. ^{{harvtxt|Foley|van Dam|Feiner|Hughes|1991|pp=207–208,216–217}}

References

{{ citation | first1 = James D. | last1 = Foley | first2 = Andries | last2 = van Dam | first3 = Steven K. | last3 = Feiner | first4 = John F. | last4 = Hughes | year = 1991 | isbn = 0-201-12110-7 | title = Computer Graphics: Principles and Practice | edition = 2nd | publisher = Addison-Wesley | location = Reading }}

3 : Matrices|Linear algebra|Sparse matrices

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Properties

Applications

See also

Notes

References