罗尔中值定理lu-oar zhongzhi dingli
若函数f (x)满足条件❶在闭区间 [a,b ]上连续;
❷在开区间 (a,b)内可导;
❸在这区间端点的函数值相等,即f (a) =f (6),则在 (a,6) 内至少存在一点c,使得f ′ (c) =0.
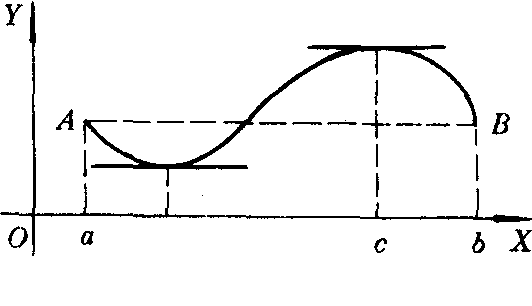
罗尔定理的几何意义如图所示.它表明,若连续曲线y=f (x)的弧AB上处处具有不垂直于x轴的切线,且两端点的纵坐标相等,则这弧上至少存在一点,使曲线在该点处的切线平行于X轴.
罗尔定理的三个条件都是重要的,如缺少其中的任何一个,定理的结论将不一定成立.例如,函数f (x)=x满足条件❶,
❷,但f (0) ≠,(1),f′ (x)=1,故结论不成立. 当然,也容易举例说明,即使定理的条件不全具备,也可能存在这样的点c,使f ′ (c) = 0.所以定理的条件是充分的,但不是必要的.