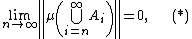- Definitions and first consequences
- Examples
- The variation of a vector measure
- Lyapunov's theorem
- References Books
- See also
In mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of finite measure, which takes nonnegative real values only.
Definitions and first consequences
Given a field of sets  and a Banach space
and a Banach space  , a finitely additive vector measure (or measure, for short) is a function
, a finitely additive vector measure (or measure, for short) is a function  such that for any two disjoint sets
such that for any two disjoint sets  and
and  in
in  one has
one has
A vector measure  is called countably additive if for any sequence
is called countably additive if for any sequence  of disjoint sets in
of disjoint sets in  such that their union is in
such that their union is in  it holds that
it holds that
with the series on the right-hand side convergent in the norm of the Banach space 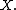
It can be proved that an additive vector measure  is countably additive if and only if for any sequence
is countably additive if and only if for any sequence  as above one has
as above one has
where  is the norm on
is the norm on 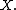
Countably additive vector measures defined on sigma-algebras are more general than finite measures, finite signed measures, and complex measures, which are countably additive functions taking values respectively on the real interval  the set of real numbers, and the set of complex numbers.
the set of real numbers, and the set of complex numbers.
Examples
Consider the field of sets made up of the interval 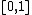 together with the family
together with the family  of all Lebesgue measurable sets contained in this interval. For any such set
of all Lebesgue measurable sets contained in this interval. For any such set  , define
, define
where  is the indicator function of
is the indicator function of  Depending on where
Depending on where  is declared to take values, we get two different outcomes.
is declared to take values, we get two different outcomes.
-
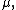 viewed as a function from
viewed as a function from  to the Lp-space
to the Lp-space  is a vector measure which is not countably-additive.
is a vector measure which is not countably-additive. -
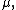 viewed as a function from
viewed as a function from  to the Lp-space
to the Lp-space  is a countably-additive vector measure.
is a countably-additive vector measure.
Both of these statements follow quite easily from the criterion (*) stated above.
The variation of a vector measure
Given a vector measure  the variation
the variation  of
of  is defined as
is defined as
where the supremum is taken over all the partitions
of  into a finite number of disjoint sets, for all
into a finite number of disjoint sets, for all  in
in  . Here,
. Here,  is the norm on
is the norm on 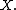
The variation of  is a finitely additive function taking values in
is a finitely additive function taking values in  It holds that
It holds that
for any  in
in  If
If  is finite, the measure
is finite, the measure  is said to be of bounded variation. One can prove that if
is said to be of bounded variation. One can prove that if  is a vector measure of bounded variation, then
is a vector measure of bounded variation, then  is countably additive if and only if
is countably additive if and only if  is countably additive.
is countably additive.
Lyapunov's theorem
In the theory of vector measures, Lyapunov's theorem states that the range of a (non-atomic) vector measure is closed and convex.[1][2][3] In fact, the range of a non-atomic vector measure is a zonoid (the closed and convex set that is the limit of a convergent sequence of zonotopes).[2] It is used in economics,[4][5][6] in ("bang–bang") control theory,[1][3][7][11] and in statistical theory.[8]
Lyapunov's theorem has been proved by using the Shapley–Folkman lemma,[9] which has been viewed as a discrete analogue of Lyapunov's theorem.[8][10]
[11]References
2. ^1 {{cite book | last1 = Diestel | first1 = Joe | last2 = Uhl | first2 = Jerry J., Jr. | title = Vector measures | publisher = American Mathematical Society | location = Providence, R.I | year = 1977 | pages = | isbn = 0-8218-1515-6}}
3. ^1 {{Cite book | title=Functional analysis and control theory: Linear systems|last=Rolewicz |first=Stefan|year=1987| isbn=90-277-2186-6| publisher=D. Reidel Publishing Co.; PWN—Polish Scientific Publishers|oclc=13064804|edition=Translated from the Polish by Ewa Bednarczuk|series=Mathematics and its Applications (East European Series)|location=Dordrecht; Warsaw|volume=29|pages=xvi+524|mr=920371| ref=harv | postscript={{inconsistent citations}}}}
4. ^{{Cite book|last=Roberts|first=John|authorlink=Donald John Roberts|chapter=Large economies|title=Contributions to the New Palgrave|editor=David M. Kreps|editor1-link=David M. Kreps|editor2=John Roberts|editor2-link=Donald John Roberts|editor3=Robert B. Wilson|editor3-link=Robert B. Wilson|date=July 1986|pages=30–35|url=https://gsbapps.stanford.edu/researchpapers/library/RP892.pdf|accessdate=7 February 2011|series=Research paper|volume=892|publisher=Graduate School of Business, Stanford University|location=Palo Alto, CA|id=(Draft of articles for the first edition of New Palgrave Dictionary of Economics)|ref=harv|postscript={{inconsistent citations}}}}
5. ^{{cite journal|authorlink=Robert Aumann|first=Robert J.|last=Aumann|title=Existence of competitive equilibrium in markets with a continuum of traders|journal=Econometrica|volume=34|number=1|date=January 1966|pages=1–17|jstor=1909854 | mr = 191623|doi=10.2307/1909854}} This paper builds on two papers by Aumann:
{{cite journal||title=Markets with a continuum of traders|journal=Econometrica|volume=32|number=1–2|date=January–April 1964|pages=39–50|jstor=1913732 | mr = 172689|doi=10.2307/1913732}}
{{cite journal||title=Integrals of set-valued functions|journal=Journal of Mathematical Analysis and Applications|volume=12|number=1|date=August 1965|pages=1–12|doi=10.1016/0022-247X(65)90049-1|mr=185073}}
6. ^{{cite news|last=Vind|first=Karl|date=May 1964|title=Edgeworth-allocations in an exchange economy with many traders|journal=International Economic Review|volume=5|pages=165–77|number=2|ref=harv|jstor=2525560}} Vind's article was noted by {{harvtxt|Debreu|1991|p=4}} with this comment:
The concept of a convex set (i.e., a set containing the segment connecting any two of its points) had repeatedly been placed at the center of economic theory before 1964. It appeared in a new light with the introduction of integration theory in the study of economic competition: If one associates with every agent of an economy an arbitrary set in the commodity space and if one averages those individual sets over a collection of insignificant agents, then the resulting set is necessarily convex. [Debreu appends this footnote: "On this direct consequence of a theorem of A. A. Lyapunov, see {{harvtxt|Vind|1964}}."] But explanations of the ... functions of prices ... can be made to rest on the convexity of sets derived by that averaging process. Convexity in the commodity space obtained by aggregation over a collection of insignificant agents is an insight that economic theory owes ... to integration theory. [Italics added]{{cite news|title=The Mathematization of economic theory|first=Gérard|last=Debreu|authorlink=Gérard Debreu|issue=Presidential address delivered at the 103rd meeting of the American Economic Association, 29 December 1990, Washington, DC|journal=The American Economic Review |volume=81, number 1 |date=March 1991 |pages=1–7 |jstor=2006785}}
7. ^{{cite book|title=Functional analysis and time optimal control|last1=Hermes|first1=Henry |last2=LaSalle|first2=Joseph P.|series=Mathematics in Science and Engineering|volume=56|publisher=Academic Press|location=New York—London|year=1969|pages=viii+136|mr=420366}}
8. ^1 2 {{cite news|last=Artstein|first=Zvi|title=Discrete and continuous bang-bang and facial spaces, or: Look for the extreme points|journal=SIAM Review|volume=22|year=1980|number=2|pages=172–185|doi=10.1137/1022026|jstor=2029960 | mr = 564562}}
9. ^{{cite news|last=Tardella|first=Fabio|title=A new proof of the Lyapunov convexity theorem|journal=SIAM Journal on Control and Optimization|volume=28|year=1990|number=2|pages=478–481|doi=10.1137/0328026|mr=1040471}}
10. ^{{cite book|last=Starr|first=Ross M.|authorlink=Ross Starr|chapter=Shapley–Folkman theorem|title=The New Palgrave Dictionary of Economics|editor-first=Steven N.|editor-last=Durlauf|editor2-first=Lawrence E., ed.|editor2-last=Blume|publisher=Palgrave Macmillan|year=2008|edition=Second|pages=317–318 (1st ed.)|url=http://www.dictionaryofeconomics.com/article?id=pde2008_S000107|doi=10.1057/9780230226203.1518|ref=harv}}
11. ^Page 210: {{cite news|last=Mas-Colell|first=Andreu|authorlink=Andreu Mas-Colell|title=A note on the core equivalence theorem: How many blocking coalitions are there?|journal=Journal of Mathematical Economics|volume=5|year=1978|number=3|pages=207–215|doi=10.1016/0304-4068(78)90010-1|mr=514468}}
Books
- {{Cite book
| last = Cohn
| first = Donald L.
| title = Measure theory
| place = Boston–Basel–Stuttgart
| publisher = Birkhäuser Verlag
| origyear = 1980
| year = 1997
| edition = reprint
| pages = IX+373
| url = https://books.google.com/books?id=vRxV2FwJvoAC&printsec=frontcover&dq=Measure+theory+Cohn&cd=1#v=onepage&q&f=false
| doi =
| zbl = 0436.28001
| isbn = 3-7643-3003-1
| ref = harv
| postscript = {{inconsistent citations}}
}}
- {{cite book
| last1 = Diestel
| first1 = Joe
| last2 = Uhl
| first2 = Jerry J., Jr.
| title = Vector measures
| series = Mathematical Surveys
| volume = 15
| publisher = American Mathematical Society
| location = Providence, R.I
| year = 1977
| pages = xiii+322
| isbn = 0-8218-1515-6
}}
- Kluvánek, I., Knowles, G, Vector Measures and Control Systems, North-Holland Mathematics Studies 20, Amsterdam, 1976.
- {{springerEOM|title=Vector measures|id=Vector_measure|first=D. |last=van Dulst}}
- {{cite book|last1=Rudin|first1=W|title=Functional analysis|date=1973|publisher=McGraw-Hill|location=New York|page=114}}
See also
- Bochner integral
- William Richardson (cricketer, born 1938)
- William Richardson (footballer)
- William Richardson (Mississippi politician)
- William Richardson (New South Wales cricketer)
- William Richard Townsend
- William Richard Wilkerson
- William Richard Williams
- William Richmond (physician)
- William Rickford Collett
- William Rick Singer
- William Ridgley Morris
- William Ridley (missionary)
- William Riley Hatch
- William Riley Parker Prize
- William Ritchie (moderator)
- William Ritchie Russell
- William Rittenhouse (Wisconsin)
- William Rivington Brownfield
- William Rivkin
- William R. Jacobs, Jr.
- William R. Jeffery
- William R. Jenkins Architecture & Art Library
- William R. Jordan III
- William R. Keith
- William R. Kenan