“Weil's conjecture on Tamagawa numbers”的意思、由来-开放百科全书

词条

Weil's conjecture on Tamagawa numbers

释义

History
Applications
See also
References
Further reading

In mathematics, the Weil conjecture on Tamagawa numbers is the statement that the Tamagawa number 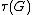of a simply connected simple algebraic group defined over a number field is 1. In this case, simply connected means "not having a proper algebraic covering" in the algebraic group theory sense, which is not always the topologists' meaning.

History

{{harvs|txt|authorlink=André Weil|last=Weil|year=1959}} calculated the Tamagawa number in many cases of classical groups and observed that it is an integer in all considered cases and that it was equal to 1 in the cases when the group is simply connected. The first observation does not hold for all groups: {{harvtxt|Ono|1963}} found examples where the Tamagawa numbers are not integers. The second observation, that the Tamagawa numbers of simply connected semisimple groups seem to be 1, became known as the Weil conjecture.

Robert Langlands (1966) introduced harmonic analysis methods to show it for Chevalley groups. K. F. Lai (1980) extended the class of known cases to quasisplit reductive groups. {{harvtxt|Kottwitz|1988}} proved it for all groups satisfying the Hasse principle, which at the time was known for all groups without E₈ factors. V. I. Chernousov (1989) removed this restriction, by proving the Hasse principle for the resistant E₈ case (see strong approximation in algebraic groups), thus completing the proof of Weil's conjecture. In 2011, Jacob Lurie and Dennis Gaitsgory announced a proof of the conjecture for algebraic groups over function fields over finite fields.{{sfn|Lurie|2014}}

Applications

{{harvtxt|Ono|1965}} used the Weil conjecture to calculate the Tamagawa numbers of all semisimple algebraic groups.

For spin groups, the conjecture implies the known Smith–Minkowski–Siegel mass formula.{{sfn|Lurie|2014}}

References

{{Springer|id=T/t092060|title=Tamagawa number}}
{{citation|last= Chernousov|first= V. I. |title=The Hasse principle for groups of type E8 |journal= Soviet Math. Dokl. |volume= 39 |year=1989|pages= 592–596|mr= 1014762}}
{{citation|last= Kottwitz|first= Robert E. |title=Tamagawa numbers |journal= Ann. of Math. |series= 2 |volume= 127 |year=1988|issue= 3|pages=629–646|doi=10.2307/2007007|jstor=2007007|publisher=Annals of Mathematics|mr= 0942522}}.
{{citation|last=Lai|first= K. F. |title=Tamagawa number of reductive algebraic groups|journal= Compositio Mathematica|volume= 41 |issue= 2 |year=1980|pages= 153–188 |url= http://www.numdam.org/item?id=CM_1980__41_2_153_0|mr=581580}}
{{citation |last=Langlands|first= R. P. |chapter=The volume of the fundamental domain for some arithmetical subgroups of Chevalley groups|year= 1966 |title= Algebraic Groups and Discontinuous Subgroups |series=Proc. Sympos. Pure Math.|pages= 143–148 |publisher=Amer. Math. Soc.|publication-place= Providence, R.I. |mr=0213362}}
{{Citation | last1=Ono | first1=Takashi | authorlink=Takashi Ono (mathematician) | title=On the Tamagawa number of algebraic tori | jstor=1970502 |mr=0156851 | year=1963 | journal=Annals of Mathematics |series=Second Series | issn=0003-486X | volume=78 | pages=47–73 | doi=10.2307/1970502}}
{{Citation | last1=Ono | first1=Takashi | title=On the relative theory of Tamagawa numbers | jstor=1970563 |mr=0177991 | year=1965 | journal=Annals of Mathematics |series=Second Series | issn=0003-486X | volume=82 | pages=88–111 | doi=10.2307/1970563}}
{{Citation | last1=Tamagawa | first1=Tsuneo | title=Algebraic Groups and Discontinuous Subgroups | publisher=American Mathematical Society | location=Providence, R.I. | series=Proc. Sympos. Pure Math. |mr=0212025 | year=1966 | volume=IX | chapter=Adèles | pages=113–121}}
{{citation|first=V. E.|last= Voskresenskii|title=Algebraic Groups and their Birational Invariants|series= AMS translation|year= 1991}}
{{Citation | last1=Weil | first1=André | author1-link=André Weil | title=Exp. No. 186, Adèles et groupes algébriques | url=http://www.numdam.org/item?id=SB_1958-1960__5__249_0 | series=Séminaire Bourbaki | year=1959 | volume=5 | pages=249–257}}
{{Citation | last1=Weil | first1=André | author1-link=André Weil | title=Adeles and algebraic groups | origyear=1961 | url=https://books.google.com/books/about/Adeles_and_algebraic_groups.html?id=vQvvAAAAMAAJ | publisher=Birkhäuser Boston | location=Boston, MA | series=Progress in Mathematics | isbn=978-3-7643-3092-7 |mr=670072 | year=1982 | volume=23}}
{{Citation | last=Lurie | first=Jacob | author-link=Jacob Lurie | title=Tamagawa Numbers via Nonabelian Poincaré Duality | year=2014 | url=http://www.math.harvard.edu/~lurie/282y.html }}

History

Applications

See also

References

Further reading