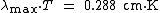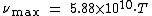- Details
- Relation to Planck's law
- Other approximations of thermal radiation
- See also
- References
Details
Wien derived his law from thermodynamic arguments, several years before Planck introduced the quantization of radiation. Details are contained in a 2009 paper by J.Crepeau entitled "A Brief History of the T4 Radiation Law".[4] The law may be written as
[5]
where
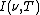 is the amount of energy per unit surface area per unit time per unit solid angle per unit frequency emitted at a frequency ν.
is the amount of energy per unit surface area per unit time per unit solid angle per unit frequency emitted at a frequency ν.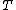 is the temperature of the black body.
is the temperature of the black body. is Planck's constant.
is Planck's constant. is the speed of light.
is the speed of light. is Boltzmann's constant.
is Boltzmann's constant.
This equation may also be written as
[3][6]
where 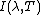 is the amount of energy per unit surface area per unit time per unit solid angle per unit wavelength emitted at a wavelength λ.
is the amount of energy per unit surface area per unit time per unit solid angle per unit wavelength emitted at a wavelength λ.
The peak value of this curve, as determined by taking the derivative and solving for zero, occurs at a wavelength λmax and frequency νmax of:[7]
in cgs units.
Relation to Planck's law
The Wien approximation was originally proposed as a description of the complete spectrum of thermal radiation, although it failed to accurately describe long wavelength (low frequency) emission. However, it was soon superseded by Planck's law, developed by Max Planck. Unlike the Wien approximation, Planck's law accurately describes the complete spectrum of thermal radiation. Planck's law may be given as
[5]
The Wien approximation may be derived from Planck's law by assuming 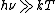 . When this is true, then
. When this is true, then
[5]
and so Planck's law approximately equals the Wien approximation at high frequencies.
Other approximations of thermal radiation
The Rayleigh–Jeans law developed by Lord Rayleigh may be used to accurately describe the long wavelength spectrum of thermal radiation but fails to describe the short wavelength spectrum of thermal emission.[3][5]
See also
- ASTM Subcommittee E20.02 on Radiation Thermometry
- Sakuma–Hattori equation
- Ultraviolet catastrophe
- Wien's displacement law
References
2. ^{{cite book |last1=Mehra |first1=J. |last2=Rechenberg |first2=H. |year=1982 |title=The Historical Development of Quantum Theory |volume=Vol. 1 |at=Chapter 1 |publisher=Springer-Verlag |isbn=978-0-387-90642-3 |ref=harv}}
3. ^1 2 3 {{cite book |last1=Bowley |first1=R. |last2=Sánchez |first2=M. |year=1999 |title=Introductory Statistical Mechanics |edition=2nd |publisher=Clarendon Press |isbn=978-0-19-850576-1 |ref=harv}}
4. ^{{cite conference |last=Crepeau |first=J. |year=2009 |title=A Brief History of the T4 Radiation Law |conference=ASME 2009 Heat Transfer Summer Conference |publisher=ASME |volume=Vol. 1 |issue= |pages=59–65 |doi=10.1115/HT2009-88060 |isbn=978-0-7918-4356-7 |ref=harv}}
5. ^1 2 3 {{cite book |last1=Rybicki |first1=G. B. |last2=Lightman |first2=A. P. |year=1979 |title=Radiative Processes in Astrophysics |publisher=John Wiley & Sons |isbn=978-0-471-82759-7 |ref=harv}}
6. ^{{cite book |last=Modest |first=M. F. |year=2013 |title=Radiative Heat Transfer |publisher=Academic Press |isbn=978-0-12-386944-9 |pages=9, 15}}
7. ^{{cite book |last1=Irwin |first1=J. A. |year=2007 |title=Astrophysics: Decoding the Cosmos |url=https://books.google.com/books?id=7SbN3iyoNf0C&pg=PA130 |page=130 |publisher=John Wiley & Sons |isbn=978-0-470-01306-9 |ref=harv}}
- Stanleyville, North Carolina
- Stanley Vincent
- Stanley Wagner (ice hockey)
- Stanley Waita
- Stanley Walker (cricketer)
- Stanley Wardley
- Stanley Watts
- Stanley W. Davenport
- Stanley Webb Davies
- Stanley Webster
- Stanley Weinbaum
- Stanley Weinberg
- Stanley Weintraub
- Stanley Weir
- Stanley Weiss
- Stanley Wellington Finch
- Stanley Wells
- Stanley Weston
- Stanley, West Yorkshire
- Stanley Whitehead
- Stanley-Whitman House
- Stanley Whittingham
- Stanley William Hayter
- Stanley William McInnis
- Stanley Williams (ballet)