轨迹命题的证明guiji mingti de zhengming

证明轨迹命题“适合条件C的点的轨迹L是图形F”，实质上是证明两个点集相等的问题.事实上，轨迹L可以看作是一个用性质说明的点集，图形F可以看作是用形象表示的点集.要证明“适合条件C的点的轨迹L是图形F”，就是证明集合L等于集合F.根据两个集合相等的定义，必须证明L⊆F及F⊆L.这两个命题又各有两种证法.要证F⊆L，可以在

A∈F⇒A∈L　(1)

及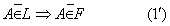

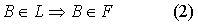
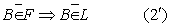
中选证一个（两者互为逆否命题）.要证L⊆F，可以在

及

中选证一个.
上面的(1)表示F上的点都有性质C,(1′)表示没有性质C的点都不在F上.它们表示F上的点全是合乎条件的点，即轨迹的纯粹性.上面的(2)表示有性质C的点都在F上，(2′)表示F以外没有具有性质C的点.它们表示F把具有性质C的一切点都包括进来了，一个也没有漏掉，即轨迹的完备性.因此，证明轨迹命题一定要确实做到以下两步：
❶在图形F上任取一点A，证明它合乎条件C;

❷任取合乎条件C的一点A′，证明它在图形F上.
有时，也可以分别改证它们的逆否命题：
❶′任一不合条件C的点B′不在图形F上；

❷′在图形F外的任一点B不合条件C.
由于证纯粹性时可证(1)或(1′)，证完备性时可证(2)或(2′)，所以证轨迹命题时，可在下列四种证法中，任择其一：❶证(1)和(2);
❷证(1)和(2′);
❸证(1′)和(2);
❹证(1′)和(2′).
至于哪一种证法方便，需要根据具体问题来定.一般地说，对于(1′)和(2′)，初学者往往感到比较困难，所以如果(1)和(2)的证明不太困难时，应尽量先选用第一种证法.
例如：一动点到一已知矩形的一组相对顶点的距离和等于它到另一组相对顶点的距离和，那么该点的轨迹是矩形的两条对称轴.

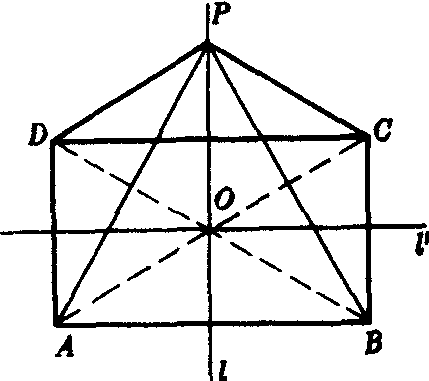
已知 如图，l和l′是矩形ABCD的两条对称轴，P点适合条件

PA+PC=PB+PD　(3)

求证 P点的轨迹是l和l′两条直线.
证明　纯粹性
在l或l′上任取一点P，因为l,l′为矩形ABCD的对称轴，所以有

PA=PB,PC=PD　(4)

或 PA=PD,PC=PB　(5)
由(4)或(5)都可得(3)，故P点合乎条件.
完备性
假定Q点合条件，即有

QA+QC=QB+QD　(6)

将(6)式两边平方，得
QA²+2QA·QC+QC²＝QB²+2QB·QD+QD² (7)
根据三角形的边与中线的关系，有

但是AC=BD.因此

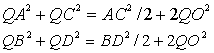
QA²+QC²＝QB²+QD²　(8)

(7)式减去(8)式，再除以2，得

QA·QC=QB·QD

改写为

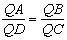
与

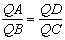
因而有

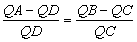
且

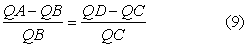
由 (6) 知

QA-QD=QB-QC

且

QA-QB=QD-QC.

假如这两个等式左右端同时为零，则Q点就是O点.
不然的话，由(9)可得

QD=QC

或

QB=QC.

这样Q点一定在l或l′上.
经过以上证明，可知本题成立.