递归论

又称“递归函数论”、“能行性理论”，指主要用数学方法研究“可构造性”、“能行可计算性”或“能行过程”的学科。各种递归函数本身的构造也是它研究的重要方面。它既属于数理逻辑的一个分支学科，又属于基础数学的一个分支学科。
递归论的主要内容包括原始递归函数，一般递归函数，部分递归函数，递归可枚举性，判定问题，递归不可解性理论，a可递归论，谱系理论等。
递归论的主要方法是通过对数论函数的研究，揭示能行过程的本质，从而解决许多重要的数学问题。递归论对数论函数的研究从原始递归函数开始，进而推广为一般递归函数，并发现一般递归函数与能行可计算函数是可以相互定义的，凡是有一个计算过程或一个算法可以将函数值计算出来的函数都是一般递归函数。
递归论所研究的数论函数都是有精确的数学定义，定义是以递归的方式进行的。例如，用递归定义式定义“斐博那奇函数”如下：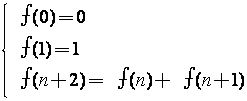

通过上面的定义，对任意一个自然数n,f_(n)恒可使用上述步骤逐步地取得。
在历史上，对于“能行过程”这一含糊的概念有过许多定义，如一般递归式、图灵机器、正规算法、有限自动机等。通过递归论的研究，发现这些定义彼此都是等价的。从这点可以看出，深入研究递归论对于弄清“能行过程”是十分关键的。
在这一领域里作出重要贡献的有希尔伯特、哥德尔、邱吉(A·Church)图灵(A·M·Turing)、克林尼(S·C·Kleene)、波斯特(E·L·Post)等人。
递归论不仅在数学基础的研究方面有极其重要的应用，而且在许多新兴的科学，尤其在电子计算机科学中已愈来愈显示出它的重要性。