闭区间上连续函数的基本性质biqujian shanglianxuhanshu de jiben xingzhi
❶最大值最小值定理 若函数f (x)在闭区间 [a,b]上连续,则函数f (x)在[a,b]上有最大值与最小值.即存在x1 ,x2 ∈〔 [a,b] ,使得对于一切x∈[a,b],总有f (x1)≤f(x)≤f (x2)。
推论 (有界性定理) 若函数f (x)在闭区间[a,b]上连续,则函数f (x)在 [a,b]上有界。
❷介值定理 若函数f (x)在闭区间 [a,b]上连续,且f (a) ≠f (b),则对于f (a)与f (b)之间的任意一个数c,在 (a,6)内至少存在一点x0 ,使得f (x0) =c。
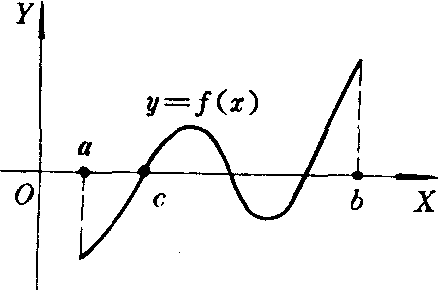
推论1 (根的存在性定理) 若函数f (x)在闭区间[a,b]上连续,且f (a) f (b)<0,则在区间 (a,b) 内至少存在一点c,使得f (c) = 0。
推论2 若函数f (x)在闭區间 [a,b]上连续,则f (x) 的值域为闭区间 [m,M],其中M,m分别为f (x)在 [a,b]上的最大值和最小值。
以上性质都具有明显的几何意义。如根的存在性定理的几何意义是,若点A (a ,f (a)) 与B (b,f (b))分别在X轴的上下两侧,则连结A,B的连续曲线y=f (x)与X轴至少有一个交点 (如上图)。