零ling
从基数的观点是把空集的基数定义为零，记作“0”.从序数的观点，是把0看成1的先行者(0本身不是自然数)并入自然数集构成扩大的自然数集.在扩大的自然数集中，规定a+0=0+a=a;a·0=0·a=0.并规定0小于一切自然数.则自然数的基本运算律和大小比较法则在扩大的自然数集中仍然成立.
在有理数集和实数集中，0又可以看成是正数和负数的分界点.
零ling
记作“0”。“没有任何东西”，可以用0来表示。任何空集的元素的个数为0。“零”，作为一个独立的数，不仅可以表示“没有”，还可以作为某些数量的界线。例如，在数轴上，它是正数与负数的界限；在摄氏温度计上，它又是零上温度与零下温度的界限；在教幼儿认识“零”时，不能说“零就是没有”，而应说“没有可以用零来表示”。
零Ling
空集的标记，表示一个集合不含任何元素。按照基数理论，自然数是有限等价集合共同特征的标记，或者说，自然数表示集合里元素的个数。用自然数表示集合的元素个数时，集合里至少得有一个元素。空集是不含任何元素的集合， 为了表示空集的共同特征，数学中引进了一个新的数——零(通常写作“0”)。零是空集的基数。例如，教室里一个学生也没有，我们就可以说教室里有0个人。零是一个有确定意义的数。因为自然数列最前面的一个数是1, 自然数列里不包括零，所以零不是自然数。如果把零和自然数列排在一起，因为零表示空集合的基数，我们可以把它排在自然数1的前面， 零小于一切自然数。零作为一个独立的数，不仅可以表示“没有”即不含任何元素，还可以用它作为某些数量的界限，例如，在数学中为了表示具有相反意义的量， 引入了负数， 正数和负数的界限就用“零”来表示，比零大的数为正数，比零小的数为负数。
零Ling
看上去极为简单的0，实际上包含着十分丰富的内容，人类对它的认识也经历了漫长的岁月。
当人们原来拥有一些物品，后来用完了，失去了，就会产生“无”的观念，在东方与西方各古代文明的早期哲学中，都不同程度地探讨过“有无”问题，中国春秋战国时代的《老子》就曾提出过“有无相生”这一著名命题。但是，认识到“无”与认识到作为数的“零”完全是两回事，实际上，在中国古代以及古代巴比伦、埃及、希腊的数学中，从来没有对作为数的零给予过讨论。
数学中现在使用的0，实际上包含了两层含义：作为位值制记数法中表示空位的记号；作为一个独立的、有表值及运算功能的数。零最初是在第一种意义上被引入数学的， 它是位值制记数法的产物。
早在公元前1900——前1600年， 巴比伦人就建立了他们的60进位值制记数系统， 但在很长的时期都没有发明表示空位的记号，于是， 
可以表示60+20=80，也可能表示602+20=3 620，或者表示602+20×60=4 800，后来他们用留空位的办法表示数字中间某位上没有数， 例如把11×602+5=39 605写作
，但这样仍然经常引起混乱，其含义往往需要通过上下文才能加以确定。直到公元前2世纪， 他们才发明了一个表示数字中某位是空位的记号， 
例如2×602+0×60+4=7 204被写作 
，但是， 这个符号也并不用在数字的末尾， 因此，
表示的到底是60+13=73，还是602+13×60=4 380, 仍然是不清楚的。
公元2世纪， 希腊天文学家、数学家托勒密(Ptolemy) 在天文学中使用巴比伦人的60进位制时，把空位记号写成了○, 可以用在一个数字的中间或末尾， 例如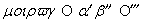
表示我们今天所说的角度0°1′2″0′″, 其中μolρ ωυ是希腊文“单位”。但这种记法仅用于天文学中，而且仅限于60进制， 并没有作为一般记数系统的一部分。
在中国古代， 至迟到公元前5世纪已经形成了利用算筹记数与计算的较为完整的系统(参见“中国古代数学”)。表示数字1——9的筹码有纵横两种方式，记数时个位用纵式，其余各位纵横相间，遇空位则不摆放算筹，例如340567被表示为☰
。由于纵横相间记数方法及空位的使用， 不必引入专门的零号就可以清楚地表示一切整数 （负数在末尾的筹码上加一斜线），因此在中国古代数学中直到金代(1180)才有了明确记载的零号，是一个正圆○，据考证来自古书中表示缺字的记号□。由于在金代以前没有表示零的记号， 因此作为数的零也就一直没有出现过。
最早在十进位值制记数系统中引入零号并且把零作为一个独立的数进行讨论的是印度人。公元四、五世纪以后，印度数码中零的符号日益明确，记数系统逐渐成为十进位值制的完备系统 (参见“印度-阿拉伯数码”)。公元628年， 印度数学家婆罗摩笈多 （参见该条）首次明确讨论了零的运算性质，包括它的加、减、乘、除运算，但是关于零能否作除数以及结果如何，在当时显然是不清楚的， 直到9世纪的摩诃毗罗(Mahavira)仍然写道： “一个数乘零得零，加零、减零或除以零，这个数都不变。”直到12世纪，婆什迦罗才正确地认识了这一问题。在讨论了关于零的加、减、乘运算后，他指出：“一个数除以零便成为一个分母为零的分数， 例如3除以0得3/0, 这个分母是符号0的分数， 称为无限大量。”但是他又错误地认为a/0×0=a。关于最这一问题， 实际上直到微积分创立以后才有可能得到真正明确而深刻的认识。
至于“零”字在古汉语中的含义，最初是指暴雨之后的小雨滴，后来引伸为“零头”、“奇零”之义，到宋代数学书中出现了表示空位的记号○，“零”字才逐渐成为空位记号的读法， 并最终具有了数字0的含义。