马铃薯叶甲Colorado potato beetle
Leptinotarsadecemlineata(Say),又称马铃薯甲虫。昆虫纲,鞘翅目,叶甲科。中国对外植物检疫对象。分布于美国、加拿大、墨西哥、比利时、荷兰、瑞士、德国、西班牙、意大利、奥地利、法国、罗马尼亚、波兰、捷克、斯洛伐克、匈牙利、俄罗斯、土耳其。寄主为马铃薯及其他茄科植物(如番茄)。成虫、幼虫均食害马铃薯叶片或顶尖,引起死苗减产。成虫体长约10 mm,黄色或橙黄色,头部、前胸、腹部有黑色斑点,鞘翅上有黑色条纹。幼虫腹部膨胀而高度隆起,似金龟甲幼虫、体砖红色。在美国一年发生1~2代。以成虫在土内越冬。成虫产卵于叶背。宜加强检疫,防止传入。
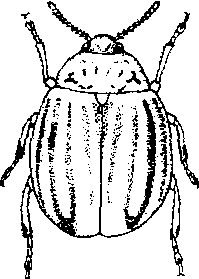
马铃薯甲虫
马铃薯叶甲
鞘翅目叶甲科。体中小型,体长9—12毫米。本色从亮橙黄色至淡黄色,头部,前胸背板,体下方和足具黑斑,每1鞘翅具5条黑带。国际性检疫害虫,20世纪80年代末期传入新疆伊犁等地。