二项分布erxiangfenbu
指一种随机事件只有两种可能结果的概率分布。比如任选一个学生，只可能出现“男生”或“女生”这两种结果之一；完全凭猜测来回答一道正误题，只可能出现“做对”或“做错”这两种结果之一。设随机事件只有两种可能结果。一种可能结果的概率为p，另一种的概率为q(q=1-p)，如果这种随机事件出现n次，则下式的数学展开式的分布就称为二项分布：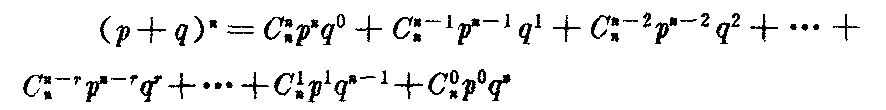
式中Cnn、Cnn-1、…是数学上的“组合”符号，其一般式为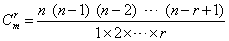
上式表示从n个元素中任取出r个元素来组合。当r=n或r=n-1时，则为Cnnn或Cnn-1。余类推。
据组合的关系式有Cn-rn＝Crn(如Cnn-2=C2n)及任何数的0次幂均为1的原理，二项分布式可写成：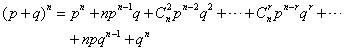
二项分布是一种离散型（即非连续型）的概率分布。当p=q=1/2、且np≥5时，它近似于正态分布；当p≠q时，它为“偏态”分布，它的平均数和标准差分别为：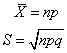
[例] 解10道正误题，学生全凭猜测作答的平均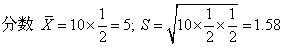
二项分布的优点是可以简捷地确定两种可能结果的各种概率。如在学生解10道正误题时，答对多少题才不是凭猜测而是凭自己真实知识得分呢？根据概率概念及二项分布公式有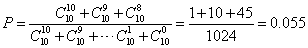
即考生凭猜测答对8题以上的概率约为5.5%，这几乎是一个小概率(通常5%以下称为小概率)，是不大可能出现的。故考生答对8题以上才认为不是凭猜测得分。由二项分布的对称性可知，考生答对2题以下也是不可能出现的小概率事件。
二项分布erxiang fenbu
在n重贝努利试验中，设每次试验某事件A出现的概率为p，令X是n次试验中事件A出现的次数，则X是一个离散型的随机变量，它的概率分布为
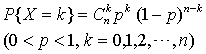
这个概率分布通常称为二项分布(因由二项式(p+q)n展开的各项组成).其中n,p为参数.当一个随机变量X的概率分布为二项分布时，称X服从参数为n,p的二项分布，记作X～B (n,p).
二项分布
一种常见的重要概率分布。在每次试验的条件相同的n次重复试验中，如果 一次试验发生某事件的概率为p，那么此事件发生k次的概率为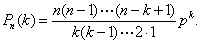
(1-p)n-k(k=0,1，…，n)，这就是二项分布的具体表示式。
二项分布
一种离散型随机变量的分布。设在一次试验中事件A出现的概率为p(0
P(X=k)=
pk(1-p)n-k, k=0,1,2，…，n
则称X的分布是参数为n,p的二项分布，记为X~b(n,p)。常被应用于测验分数统计中。
二项分布binomial distribution
概率论中关于二项式n次乘幂的概率分布。描述随机现象的一种常用分布。整个总体中，仅有两种可能结果时，如种子的发芽与不发芽、产品的合格与不合格等，假定在一次抽样试验中，两种结果出现的概率分别为p和q，则p+q=1。在n次重复的试验中，则这两组出现次数不同的组合，构成如下的概率分布：
