- Differential form
- Integral form
- Vector potential
- Field lines
- Modification if magnetic monopoles exist
- History
- See also
- References
In physics, Gauss's law for magnetism is one of the four Maxwell's equations that underlie classical electrodynamics. It states that the magnetic field {{math|B}} has divergence equal to zero,[1] in other words, that it is a solenoidal vector field. It is equivalent to the statement that magnetic monopoles do not exist.[2] Rather than "magnetic charges", the basic entity for magnetism is the magnetic dipole. (If monopoles were ever found, the law would have to be modified, as elaborated below.)
Gauss's law for magnetism can be written in two forms, a differential form and an integral form. These forms are equivalent due to the divergence theorem.
The name "Gauss's law for magnetism"[1] is not universally used. The law is also called "Absence of free magnetic poles";[2] one reference even explicitly says the law has "no name".[3] It is also referred to as the "transversality requirement"[4] because for plane waves it requires that the polarization be transverse to the direction of propagation.
Differential form
The differential form for Gauss's law for magnetism is:
{{Equation box 1|indent =:
|equation =

|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
where {{math|∇ ·}} denotes divergence, and {{math|B}} is the magnetic field.
Integral form
The integral form of Gauss's law for magnetism states:
{{Equation box 1|indent =:
|equation = {{oiint|intsubscpt=
 |integrand=
|integrand=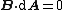 }}
}}|cellpadding= 15
|border
|border colour = #0073CF
|background colour=#F5FFFA}}
where {{math|S}} is any closed surface (see image right), and {{math|dA}} is a vector, whose magnitude is the area of an infinitesimal piece of the surface {{math|S}}, and whose direction is the outward-pointing surface normal (see surface integral for more details).
The left-hand side of this equation is called the net flux of the magnetic field out of the surface, and Gauss's law for magnetism states that it is always zero.
The integral and differential forms of Gauss's law for magnetism are mathematically equivalent, due to the divergence theorem. That said, one or the other might be more convenient to use in a particular computation.
The law in this form states that for each volume element in space, there are exactly the same number of "magnetic field lines" entering and exiting the volume. No total "magnetic charge" can build up in any point in space. For example, the south pole of the magnet is exactly as strong as the north pole, and free-floating south poles without accompanying north poles (magnetic monopoles) are not allowed. In contrast, this is not true for other fields such as electric fields or gravitational fields, where total electric charge or mass can build up in a volume of space.
Vector potential
{{main|Magnetic vector potential}}Due to the Helmholtz decomposition theorem, Gauss's law for magnetism is equivalent to the following statement:[5][6]
{{block indent|1=There exists a vector field {{math|A}} such that{{block indent|1= .}}}}
.}}}}The vector field {{math|A}} is called the magnetic vector potential.
Note that there is more than one possible {{math|A}} which satisfies this equation for a given {{math|B}} field. In fact, there are infinitely many: any field of the form {{math|∇ϕ}} can be added onto {{math|A}} to get an alternative choice for {{math|A}}, by the identity (see Vector calculus identities):
{{block indent|1= }}
}}since the curl of a gradient is the zero vector field:
{{block indent|1= }}
}}This arbitrariness in {{math|A}} is called gauge freedom.
Field lines
{{main|Field line}}The magnetic field {{math|B}}, like any vector field, can be depicted via field lines (also called flux lines) – that is, a set of curves whose direction corresponds to the direction of {{math|B}}, and whose areal density is proportional to the magnitude of {{math|B}}. Gauss's law for magnetism is equivalent to the statement that the field lines have neither a beginning nor an end: Each one either forms a closed loop, winds around forever without ever quite joining back up to itself exactly, or extends to infinity.
Modification if magnetic monopoles exist
{{main|Magnetic monopole}}If magnetic monopoles were discovered, then Gauss's law for magnetism would state the divergence of {{math|B}} would be proportional to the magnetic charge density {{math|ρm}}, analogous to Gauss's law for electric field. For zero net magnetic charge density ({{math|1=ρm = 0}}), the original form of Gauss's magnetism law is the result.
The modified formula in SI units is not standard; in one variation, magnetic charge has units of webers, in another it has units of ampere-meters.
| Units | Equation |
|---|---|
| cgs units[7] |  |
| SI units (weber convention)[8] |  |
| SI units (ampere-meter convention)[9] |  |
where {{math|μ0}} is the vacuum permeability.
So far no magnetic monopoles have been found, despite extensive search.[10]
History
This idea of the nonexistence of magnetic monopoles originated in 1269 by Petrus Peregrinus de Maricourt. His work heavily influenced William Gilbert, whose 1600 work De Magnete spread the idea further. In the early 1800s Michael Faraday reintroduced this law, and it subsequently made its way into James Clerk Maxwell's electromagnetic field equations.
See also
{{Wikipedia books|Maxwell's equations}}- Magnetic moment
- Vector calculus
- Integral
- Flux
- Gaussian surface
- Faraday's law of induction
- Ampère's circuital law
- Lorenz gauge condition
References
2. ^1 {{cite book |first=John David |last=Jackson |year=1999 |title=Classical Electrodynamics |page=237 |edition=3rd |publisher=Wiley |isbn=0-471-30932-X}}
3. ^{{cite book |first1=David J. |last1=Griffiths |year=1998 |title=Introduction to Electrodynamics |page=321 |edition=3rd |publisher=Prentice Hall |isbn=0-13-805326-X}}
4. ^{{cite book |first1=John D. |last1=Joannopoulos |first2=Steve G. |last2=Johnson |first3=Joshua N. |last3=Winn |first4=Robert D. |last4=Meade |year=2008 |title=Photonic Crystals: Molding the Flow of Light |page=9 |edition=2nd |publisher=Princeton University Press |isbn=978-0-691-12456-8}}
5. ^{{cite book |first1=W. H. A.|last1=Schilders |title=Handbook of Numerical Analysis |url=https://books.google.com/books?id=F_E9SAe6ny0C&pg=PA13 |page=13 |isbn=978-0-444-51375-5 |date=2005 |display-authors=etal}}
6. ^{{cite book | first=John David |last=Jackson | year=1999 | title=Classical Electrodynamics | publisher=Wiley | page=180 | edition=3rd | isbn=0-471-30932-X}}
7. ^{{cite journal|first=F.|last=Moulin|year=2001|title=Magnetic monopoles and Lorentz force|journal=Il Nuovo Cimento B|volume=116 |issue=8 |pages=869–877|arxiv=math-ph/0203043|bibcode = 2001NCimB.116..869M}}
8. ^{{cite book |first=John David |last=Jackson |year=1999 |title=Classical Electrodynamics |edition=3rd |page=273, eq. 6.150 |publisher=Wiley}}
9. ^See for example equation 4 in {{cite journal |first1=M. |last1=Nowakowski |first2=N. G. |last2=Kelkar |year=2005 |title=Faraday's law in the presence of magnetic monopoles |journal=Europhysics Letters |volume=71 |issue=3 |pages=346 |arxiv=physics/0508099 |doi=10.1209/epl/i2004-10545-2|bibcode = 2005EL.....71..346N }}
10. ^Magnetic Monopoles, report from Particle data group, updated August 2015 by D. Milstead and E.J. Weinberg. "To date there have been no confirmed observations of exotic particles possessing magnetic charge."
- Camisado (dance song)
- Camisado (Song)
- Camisado (song)
- Camisano, Lombardy
- Camisano Vicentino
- Camisas azuis
- Camisas Doradas
- Camisea Gas Project
- Camissonia
- Camissonia campestris
- Camissoniopsis cheiranthifolia
- Camito
- Cam Janssen
- Cam Jones
- CAMK2A
- CAMK2B
- CAMK4
- Camkid
- CaM Kinase
- CaM Kinase II
- Camlachie
- Camlan
- Camlann
- Camlann Medievel Vilage
- Cam Lasely