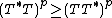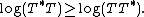“Hyponormal operator”的意思、由来-开放百科全书

词条

Hyponormal operator

释义

See also
References

In mathematics, especially operator theory, a hyponormal operator is a generalization of a normal operator. In general, a bounded linear operator T on a complex Hilbert space H is said to be p-hyponormal (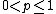) if:

(That is to say, 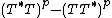is a positive operator.) If , then T is called a hyponormal operator. If 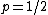, then T is called a semi-hyponormal operator. Moreoever, T is said to be log-hyponormal if it is invertible and

An invertible p-hyponormal operator is log-hyponormal. On the other hand, not every log-hyponormal is p-hyponormal.

The class of semi-hyponormal operators was introduced by Xia, and the class of p-hyponormal operators was studied by Aluthge, who used what is today called the Aluthge transformation.

Every subnormal operator (in particular, a normal operator) is hyponormal, and every hyponormal operator is a paranormal convexoid operator. Not every paranormal operator is, however, hyponormal.

References

http://www.jstor.org/pss/2162263

1 : Operator theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

References