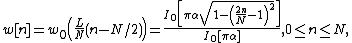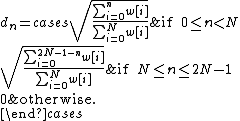“Kaiser window”的意思、由来-开放百科全书

The Kaiser window, also known as the Kaiser–Bessel window, was developed by James Kaiser at Bell Laboratories. It is a one-parameter family of window functions used in finite impulse response filter design and spectral analysis. The Kaiser window approximates the DPSS window which maximizes the energy concentration in the main lobe^[1] but which is difficult to compute^[2].

Definition

where the length of the window is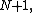

and N can be even or odd. (see Window_function#A_list_of_window_functions)

In the Fourier transform, the first null after the main lobe occurs at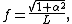

which is just

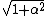in units of N (DFT "bins"). As α increases, the main lobe increases in width, and the side lobes decrease in amplitude. {{math|α}} = 0 corresponds to a rectangular window. For large {{math|α,}} the shape of the Kaiser window (in both time and frequency domain) tends to a Gaussian curve. The Kaiser window is nearly optimal in the sense of its peak's concentration around frequency 0.^[4]{{page needed|date=February 2018}}

Kaiser–Bessel-derived (KBD) window

A related window function is the Kaiser–Bessel-derived (KBD) window, which is designed to be suitable for use with the modified discrete cosine transform (MDCT). The KBD window function is defined in terms of the Kaiser window of length N+1, by the formula:

This defines a window of length 2N, where by construction d_n satisfies the Princen-Bradley condition for the MDCT (using the fact that {{math|w{{sub|N−n}} {{=}} w{{sub|n}}}}): {{math|d{{sub|n}}² + (d{{sub|n+N}})² {{=}} 1}} (interpreting n and n + N modulo 2N). The KBD window is also symmetric in the proper manner for the MDCT: d_n = d_2N−1−n.

Applications

References

1. ^{{Cite web |url=https://ccrma.stanford.edu/~jos/sasp/Slepian_DPSS_Window.html |title=Slepian or DPSS Window |website=ccrma.stanford.edu |access-date=2016-04-13}}
2. ^{{cite book |author1=Oppenheim, A. V. |author2=Schafer, R. W. |title=Discrete-time signal processing |location=Upper Saddle River, N.J. |publisher=Prentice Hall |year=2009 |page=541 |isbn=9780131988422}}
3. ^{{cite journal |ref=refHarris |doi=10.1109/PROC.1978.10837 |last=Harris |first=Fredric J. |title=On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform |journal=Proceedings of the IEEE |volume=66 |issue=1 |pages=51–83 |date=Jan 1978 |url=http://web.mit.edu/xiphmont/Public/windows.pdf|citeseerx=10.1.1.649.9880 }}
4. ^{{cite book |author1=Oppenheim, A. V. |author2=Schafer, R. W. |author3=Buck J. R. | title=Discrete-time signal processing | location=Upper Saddle River, N.J. | publisher=Prentice Hall | year=1999 | isbn=0-13-754920-2}}

Definition

Kaiser–Bessel-derived (KBD) window

Applications

References

Further reading