- Examples of Systems Simply typed lambda calculus System F Lambda-P System Fω Calculus of constructions
- Formal definition
- Comparison between the systems λ→ λ2 λP λω λC
- Relation to other systems
- Common properties
- Subtyping
- See also
- Notes
- Further reading
- External links
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt [1] to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new way of making objects depend on other objects, namely
- terms allowed to depend on types, corresponding to polymorphism.
- types depending on terms, corresponding to dependent types.
- types depending on types, corresponding to type operators.
The different ways to combine these three dimension yield the 8 vertices of the cube, each corresponding to a different kind of typed system.
Examples of Systems
Simply typed lambda calculus
The simplest system found in the λ-cube is the simply typed lambda calculus, also called λ→. In this system, the only way to construct an abstraction is by making a term depend on a term variable, with the rule
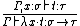
System F
In System F, also named λ2, there is another type of abstraction, written with a  , that allows terms to depend on types, with the following rule:
, that allows terms to depend on types, with the following rule:
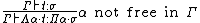
The terms beginning with a  are called polymorphic, as they can be applied to different types to get different functions, similarly to polymorphic functions in ML-like languages. For instance, the polymorphic identity
are called polymorphic, as they can be applied to different types to get different functions, similarly to polymorphic functions in ML-like languages. For instance, the polymorphic identity
fun x -> x
of OCaml has type'a -> 'a
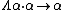 .
.Lambda-P
In the λP system, also named ΛΠ, and closely related to the Logical Framework, one has so called dependent types. These are types that are allowed to depend on terms. The crucial induction rule of the system is
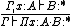
where  represents valid types. The new type constructor
represents valid types. The new type constructor  corresponds via the Curry-Howard isomorphism to a universal quantifier, and the system λP as a whole corresponds to first order logic with implication as only connective. An example of these dependent types in concrete programming is the type of vectors on a certain length: the length is a term, on which the type depends.
corresponds via the Curry-Howard isomorphism to a universal quantifier, and the system λP as a whole corresponds to first order logic with implication as only connective. An example of these dependent types in concrete programming is the type of vectors on a certain length: the length is a term, on which the type depends.
System Fω
In System Fω, one has the  constructor of System F, but another construction is allowed: types can be constructed from other types. This is called type constructors, and an example would be
constructor of System F, but another construction is allowed: types can be constructed from other types. This is called type constructors, and an example would be 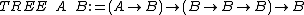 with
with  and
and  free type variable. In concrete programming, this feature corresponds to the ability to define type constructors inside the language, rather than considering them as primitives. The previous type constructor roughly corresponds to the following definition of a trees with labeled leaves in OCaml:
free type variable. In concrete programming, this feature corresponds to the ability to define type constructors inside the language, rather than considering them as primitives. The previous type constructor roughly corresponds to the following definition of a trees with labeled leaves in OCaml:
type tree = | Leaf of a | Node of 'a tree * 'a tree
Calculus of constructions
In the calculus of constructions, denoted as λC in the cube, these three features cohabit, so that both types and terms can depend on types and terms. The clear border that exists in λ→ between terms and types is somewhat abolished, as all types except the universal  are themselves terms with a type.
are themselves terms with a type.
Formal definition
As for all systems based upon the simply typed lambda calculus, all systems in the cube are given in two steps: first, raw terms, together with a notion of β-reduction, and then typing rules that allow to type those terms.
The set of sorts is defined as 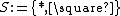 , sorts are represented with the letter
, sorts are represented with the letter  . There is also a set
. There is also a set  of variables, represented by the letters
of variables, represented by the letters 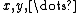 . The raw terms of the eight systems of the cube are given by the following syntax:
. The raw terms of the eight systems of the cube are given by the following syntax:
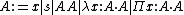
and  denoting
denoting 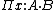 when
when  does not occur free in
does not occur free in  .
.
The environment, as is usual in typed systems, are given by
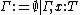
The notion of β-reduction is common to all systems in the cube. It is written 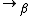 and given by the rules
and given by the rules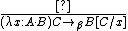

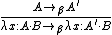

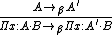 Its reflexive, transitive closure is written
Its reflexive, transitive closure is written 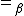 .
.
The following typing rules are also common to all systems in the cube: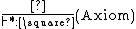
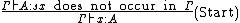
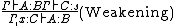
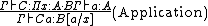
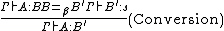 The difference between the systems is in the pairs of sorts
The difference between the systems is in the pairs of sorts 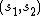 that are allowed in the following two typing rules:
that are allowed in the following two typing rules: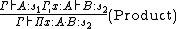
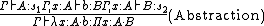
The correspondence between the systems and the pairs 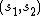 allowed in the rules is the following:
allowed in the rules is the following:
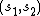 | 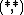 | 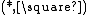 |  |  |
|---|---|---|---|---|
| λ→ | x | |||
| λP | x | x | ||
| λ2 | x | x | ||
| λω | x | x | ||
| λP2 | x | x | x | |
| λPω | x | x | x | |
| λω | x | x | x | |
| λC | x | x | x | x |
Each direction of the cube corresponds to one pair (excluding the pair 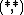 shared by all systems), and in turn each pair corresponds to one possibility of dependency between terms and types:
shared by all systems), and in turn each pair corresponds to one possibility of dependency between terms and types:
-
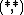 allows terms to depend on terms.
allows terms to depend on terms. -
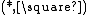 allows types to depend on terms.
allows types to depend on terms. -
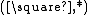 allows terms to depend on types.
allows terms to depend on types. -
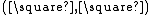 allows types to depend on types.
allows types to depend on types.
Comparison between the systems
λ→
A typical derivation that can be obtained is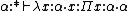 or with the arrow shortcut
or with the arrow shortcut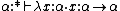 closely resembling the identity (of type
closely resembling the identity (of type  ) of the usual λ→. Note that all types used must appear in the context, because the only derivation that can be done in an empty context is
) of the usual λ→. Note that all types used must appear in the context, because the only derivation that can be done in an empty context is 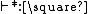 .
.
The computing power is quite weak, it corresponds to the extended polynomials (polynomials together with a conditional operator) [2].
λ2
In λ2, such terms can be obtained as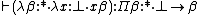 with
with 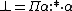 . If one reads
. If one reads  as a universal quantification, via the Curry-Howard isomorphism, this can be seen as a proof of the principle of explosion. In general, λ2 adds the possibility to have impredicative types such as
as a universal quantification, via the Curry-Howard isomorphism, this can be seen as a proof of the principle of explosion. In general, λ2 adds the possibility to have impredicative types such as  , that is terms quantifying over all types including themselves.
, that is terms quantifying over all types including themselves.
The polymorphism also allows the construction of functions that were not constructible in λ→. More precisely, the function definable in System F are those provably total in second order Peano arithmetic[3]. In particular, all primitive recursive functions are definable.
λP
In λP, the ability to have types depending on terms means one can express logical predicates. For instance, the following is derivable: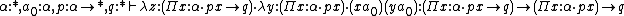 which corresponds, via the Curry-Howard isomorphism, to a proof of
which corresponds, via the Curry-Howard isomorphism, to a proof of 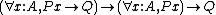 .
.
From the computational point of view, however, having dependent types does not enhance computational power, only the possibility to express more precise type properties[4].
The conversion rule is strongly needed when dealing with dependent types, because it allows to perform computation on the terms in the type. For instance, if you have 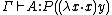 and
and 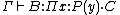 , you need to apply the conversion rule to obtain
, you need to apply the conversion rule to obtain 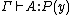 to be able to type
to be able to type 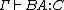 .
.
λω
In λω, the following operator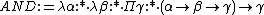 is definable, that is
is definable, that is 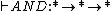 . The derivation
. The derivation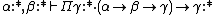 can be obtained already in λω, however the polymorphic
can be obtained already in λω, however the polymorphic 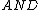 can only be defined if the rule
can only be defined if the rule 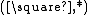 is also present.
is also present.
From a computing point of view, λω is extremely strong, and has been considered as a basis for programming languages [5].
λC
The calculus of constructions has both the predicate expressiveness of λC and the computational power of λω, so it is very powerful, both on the logical side and on the computational side.
Relation to other systems
The system Automath is similar to λ2 from a logical point of view. The ML-like languages, from a typing point of view, lie somewhere between λ→ and λ2, as they admit a restricted kind of polymorphic types, that is the types in prenex normal form. However, because they feature some recursion operators, their computing power is greater than that of λ2.[4] The Coq system is based on an extension of λC with a linear hierarchy of universes, rather than only one untypable  , and the ability to construct inductive types.
, and the ability to construct inductive types.
Pure Type Systems can be seen as a generalization of the cube, with an arbitrary set of sorts, axiom, product and abstraction rules. Conversely, the systems of the lambda cube can be expressed as Pure Type Systems with two sorts 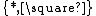 , the only axiom
, the only axiom 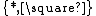 , and a set of rules
, and a set of rules  such that
such that 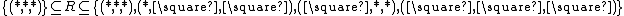 [1].
[1].
Via the Curry-Howard isomorphism, there is a one-to-one correspondence between the systems in the lambda cube and logical systems[1], namely:
| System of the cube | Logical System |
|---|---|
| λ→ | (First Order) Propositional Calculus |
| λ2 | Second Order Propositional Caculus |
| λω | Weakly Higher Order Propositional Calculus |
| λω | Higher Order Propositional Calculus |
| λP | (First Order) Predicate Logic |
| λP2 | Second Order Propositional Calculus |
| λPω | Weak Higher Order Propositional Calculus |
| λC | Calculus of Constructions |
All the logics are implicative (i.e. the only connectives are  and
and  ), however one can define other connectives such as
), however one can define other connectives such as  or
or  in an impredicative way in second and higher order logics. In the weak higher order logics, there are variables for higher order predicates, but no quantification on those can be done.
in an impredicative way in second and higher order logics. In the weak higher order logics, there are variables for higher order predicates, but no quantification on those can be done.
Common properties
All systems in the cube enjoy
- the Church-Rosser property: if
 and
and 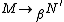 then there exists
then there exists 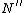 such that
such that 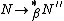 and
and 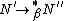 ;
; - the subject reduction property: if
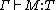 and
and 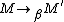 then
then 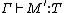 ;
; - the uniqueness of types: if
 and
and 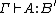 then
then 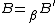 .
.
All of these can be proven on generic pure type systems[6].
Any term well-typed in a system of the cube is strongly normalizing[1], although this property is not common to all pure type systems. No system in the cube is Turing complete[4].
Subtyping
Subtyping however is not represented in the cube, even though systems like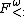 , known as higher-order bounded quantification, which combines subtyping and polymorphism are of practical interest, and can be further generalized to bounded type operators. Further extensions to
, known as higher-order bounded quantification, which combines subtyping and polymorphism are of practical interest, and can be further generalized to bounded type operators. Further extensions to 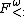 allow the definition of purely functional objects; these systems were generally developed after the lambda cube paper was published.[7]
allow the definition of purely functional objects; these systems were generally developed after the lambda cube paper was published.[7]The idea of the cube is due to the mathematician Henk Barendregt (1991). The framework of pure type systems generalizes the lambda cube in the sense that all corners of the cube, as well as many other systems can be represented as instances of this general framework.[8] This framework predates the lambda cube by a couple of years. In his 1991 paper, Barendregt also defines the corners of the cube in this framework.
See also
- In his Habilitation à diriger les recherches[9], Olivier Ridoux gives a cut-out template of the lambda cube and also a dual representation of the cube as an octahedron, where the 8 vertices are replaced by faces, as well as a dual representation as a dodecahedron, where the 12 edges are replaced by faces.
- Homotopy type theory
Notes
2. ^{{Cite journal|last=Schwichtenberg|first=Helmut|date=1975|title=Definierbare Funktionen imλ-Kalkül mit Typen|journal=Archiv für Mathematische Logik und Grundlagenforschung|volume=17|issue=3–4|pages=113–114|doi=10.1007/bf02276799|issn=0933-5846}}
3. ^{{Cite book|title=Proofs and types|last=Jean-Yves.|first=Girard|date=1989|publisher=Cambridge University Press|isbn=|location=|pages=|oclc=504959682}}
4. ^1 2 {{Cite book|title=Lambda-Prolog de A à Z ... ou presque|last=Ridoux|first=Olivier|date=1998|publisher=[s.n.]|isbn=|location=|pages=|oclc=494473554}}
5. ^{{Cite book|title=Programming in higher-order typed lambda-calculi|last=C.|first=Pierce, Benjamin|date=1989|publisher=Carnegie Mellon University, Computer Science Dept|oclc=20442222}}
6. ^{{Citation|last=Sørensen|first=Morten Heine|title=Pure type systems and the λ-cube|date=2006|work=Lectures on the Curry-Howard Isomorphism|pages=343–359|publisher=Elsevier|isbn=9780444520777|last2=Urzyczyin|first2=Pawel|doi=10.1016/s0049-237x(06)80015-7}}
7. ^{{Cite book|title=Types and programming languages|last=Pierce|first=Benjamin|date=2002|publisher=MIT Press|isbn=978-0262162098|location=|pages=467–490|oclc=300712077}}
8. ^{{Cite book|title=Types and programming languages|last=Pierce|first=Benjamin|date=2002|publisher=MIT Press|isbn=978-0262162098|location=|pages=466|oclc=300712077}}
9. ^{{Cite book|title=Lambda-Prolog de A à Z ... ou presque|last=Ridoux|first=Olivier|date=1998|publisher=[s.n.]|isbn=|location=|pages=70|oclc=494473554}}
Further reading
- Simon Peyton Jones and Erik Meijer, 1997. [https://www.microsoft.com/en-us/research/wp-content/uploads/1997/01/henk.pdf Henk: A Typed Intermediate Language]
External links
- Barendregt's Lambda Cube in the context of pure type systems by Roger Bishop Jones
- April 1909
- April 1910
- April 1920 Guatemalan presidential election
- April 1920 Nabi Musa riots in Palestine
- April 1921 lunar eclipse
- April 1924 tornado outbreak
- April 1927
- April 1943
- April 1946
- April 1950 lunar eclipse
- April 1957 Southeastern tornado outbreak
- April 1958 Florida tornado outbreak
- April 1958 lunar eclipse
- April 1959
- April 1960
- April 1961
- April 1967 lunar eclipse
- April 1968 lunar eclipse
- April 1969 lunar eclipse
- April 1971
- April 1972
- April 1977 lunar eclipse
- April 1986 lunar eclipse
- April 1987 lunar eclipse
- April 1994 tornado outbreak