作两圆的内公切线zuo liangyuan de neigongqiexian

已知 如图，⊙O和⊙O′外离，它们的半径分别为R和R′.求作 ⊙O和⊙O′的内公切线.

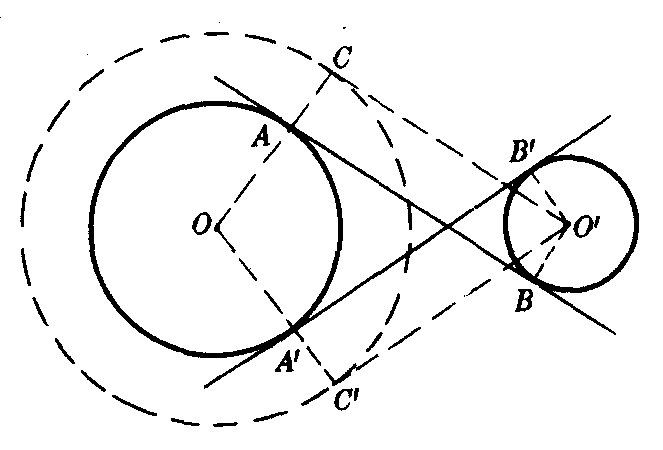
分析 设AB是所求的内公切线，A和B是切点.连结OA,O′B.则OA⊥AB,O′B⊥AB.所以OA∥O′B.过O′作O′C∥AB与OA的延长线交于C，则O′C⊥OC.因此，O′C是以O为圆心，OC为半径的圆的切线，并且OC=OA+AC=OA+O′B=R+R′.所以这个圆可以作出，因而C点位置可以确定.再根据O,C两点的位置可确定A点的位置，又根据O′B∥OA,B点的位置也可确定，于是内公切线AB可作出.
作法 ❶以O为圆心，R+R′为半径作圆；
❷过O′作这圆的切线O′C，切点为C;
❸连结OC′，交⊙O于A;
❹过O′作O′B∥OA，交⊙O′于B;
❺过A,B两点作直线.则直线AB就是所求的内公切线.
用同样的方法，可以作出另一条内公切线A′B′.
说明 ❶当两圆外切时，经过切点作直线垂直于它们的连心线，就可得到它们的内公切线；
❷当两圆外离时，可作出两条内公切线；当两圆外切时，可作出一条内公切线；当两圆相交、内切或内含时，无内公切线.