作圆的内接正十边形zuo yuan de neijie zhengshibianx-ing

分析 如图1，设A₁A₂是⊙O的内接正十边形的一边，连结OA₁,OA₂.则∠A₁OA₂＝360°/10=36°.∠OA₁A₂＝∠OA₂A₁＝(180°-36°)/2=72°.作∠OA₂A₁的平分线交OA1于M.则∠OA₂M=36°，所以∠OA₂M=∠A₂OM. 因此OM=A₂M.另一方面，∠A₁MA₂＝∠OA₂M+∠A₂OM=36°+36°=72°.所以∠A₁MA₂＝∠A₂A₁M.因此A₂M=A₁A₂.于是OM=A₁A₂.根据三角形内角平分线的性质有A₂O/A₁A₂＝OM/MA₁，即OA₁/OM=OM/MA₁.所以OM就是把OA₁分成中外比而得到的较大部分.它就等于圆内接正十边形的一边.
作法 ❶在⊙O内作半径OA1⊥OB(图2);
❷取OB中点C;
❸连结A₁C;
❹在A₁C上截取CD=CO;
❺以A₁为圆心，A₁D为半径作弧交⊙O于A₂;
❻连结A₁A₂.则A₁A₂就是圆内接正十边形的一边.顺次量取A₁A₂长，就得到圆内接正十边形的各顶点.

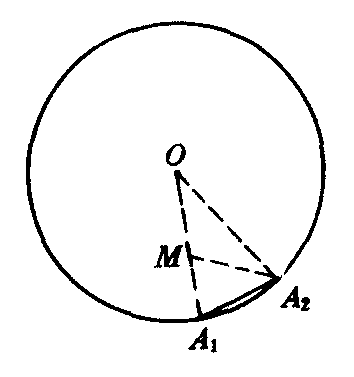
图1

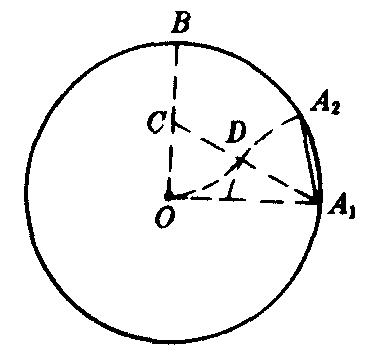
图2