“Morphological skeleton”的意思、由来-开放百科全书

词条

Morphological skeleton

释义

Skeleton by openings
Lantuéjoul's formula Continuous images Discrete images Reconstruction from the skeleton The skeleton as the centers of the maximal disks
Performing Morphological Skeletonization on Images
Notes
References

In digital image processing, morphological skeleton is a skeleton (or medial axis) representation of a shape or binary image, computed by means of morphological operators.

Morphological skeletons are of two kinds:

Those defined by means of morphological openings, from which the original shape can be reconstructed,
Those computed by means of the hit-or-miss transform, which preserve the shape's topology.

Skeleton by openings

Lantuéjoul's formula

Continuous images

In (Lantuéjoul 1977),^[1] Lantuéjoul derived the following morphological formula for the skeleton of a continuous binary image :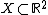

,

where and are the morphological erosion and opening, respectively, 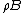is an open ball of radius , and 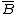is the closure of .

Discrete images

Let 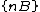, , 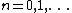be a family of shapes, where B is a structuring element,

, and

, where o denotes the origin.

The variable n is called the size of the structuring element.

Lantuéjoul's formula has been discretized as follows. For a discrete binary image 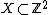, the skeleton S(X) is the union of the skeleton subsets 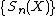, , 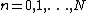where:

.

Reconstruction from the skeleton

The original shape X can be reconstructed from the set of skeleton subsets 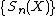as follows:

.

Partial reconstructions can also be performed, leading to opened versions of the original shape:

.

The skeleton as the centers of the maximal disks

Let 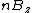be the translated version of to the point z, that is, .

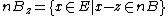A shape 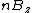centered at z is called a maximal disk in a set A when:

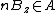, and
if, for some integer m and some point y, 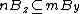, then .

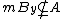Each skeleton subset 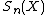consists of the centers of all maximal disks of size n.

Performing Morphological Skeletonization on Images

Morphological Skeletonization can be considered as a controlled erosion process. This involves shrinking the image until the area of interest is 1 pixel wide. This can allow quick and accurate image processing on an otherwise large and memory intensive operation. A great example of using skeletonization on an image is processing fingerprints. This can be quickly accomplished using bwmorph; a built-in Matlab function which will implement the Skeletonization Morphology technique to the image.

The image to the right shows the extent of what skeleton morphology can accomplish. Given a partial image, it is possible to extract a much fuller picture. Properly pre-processing the image with a simple Auto Threshold grayscale to binary converter will give the skeletonization function an easier time thinning. The higher contrast ratio will allow the lines to joined in a more accurate manner. Allowing to properly reconstruct the fingerprint.

Notes

1. ^See also (Serra's 1982 book)

References

Image Analysis and Mathematical Morphology by Jean Serra, {{ISBN|0-12-637240-3}} (1982)
Image Analysis and Mathematical Morphology, Volume 2: Theoretical Advances by Jean Serra, {{ISBN|0-12-637241-1}} (1988)
An Introduction to Morphological Image Processing by Edward R. Dougherty, {{ISBN|0-8194-0845-X}} (1992)
Ch. Lantuéjoul, "Sur le modèle de Johnson-Mehl généralisé", Internal report of the Centre de Morph. Math., Fontainebleau, France, 1977.
Scott E. Umbaugh (2018). Digital Image Processing and Analysis, pp 93-96. CRC Press. {{ISBN|978-1-4987-6602-9}}

2 : Mathematical morphology|Digital geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。