请输入您要查询的百科知识：

　

词条 Parikh's theorem
释义

  1. Definitions and formal statement

  2. Strengthening for bounded languages

  3. Significance

  4. References

Parikh's theorem in theoretical computer science says that if one looks only at the number of occurrences of each terminal symbol in a context-free language, without regard to their order, then the language is indistinguishable from a regular language.[1] It is useful for deciding that strings with a given number of terminals are not accepted by a context-free grammar.[2] It was first proved by Rohit Parikh in 1961[3] and republished in 1966.[4]

Definitions and formal statement

Let 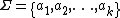be an alphabet. The Parikh vector of a word is defined as the function 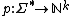, given by[1]

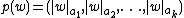
where denotes the number of occurrences of the letter in the word .

A subset of 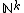is said to be linear if it is of the form

for some vectors .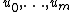

A subset of 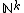is said to be semi-linear if it is a union of finitely many linear subsets.

Statement 1: Let be a context-free language.

Let 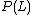be the set of Parikh vectors of words in , that is, 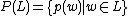. Then 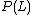is a semi-linear set.

Two languages are said to be commutatively equivalent if they have the same set of Parikh vectors.

Statement 2: If is any semi-linear set, the language of words whose Parikh vectors are in is commutatively equivalent to some regular language. Thus, every context-free language is commutatively equivalent to some regular language.

These two equivalent statements can be summed up by saying that the image under of context-free languages and of regular languages is the same, and it is equal to the set of semilinear sets.

Strengthening for bounded languages

A language is bounded if 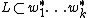for some fixed words .

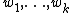Ginsburg and Spanier [5]

gave a necessary and sufficient condition, similar to Parikh's theorem, for bounded languages.

Call a linear set stratified, if in its definition for each 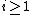the vector has the property that it has at most two non-zero coordinates, and for each 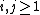if each of the vectors 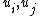has two non-zero coordinates, and 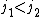, respectively, then their order is not .

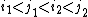A semi-linear set is stratified if it is a union of finitely many stratified linear subsets.

The Ginsburg-Spanier theorem says that a bounded language is context-free if and only if 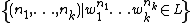is a stratified semi-linear set.

Significance

The theorem has multiple interpretations. It shows that a context-free language over a singleton alphabet must be a regular language and that some context-free languages can only have ambiguous grammars{{explain|reason=why exactly?|date=April 2017}}. Such languages are called inherently ambiguous languages. From a formal grammar perspective, this means that some ambiguous context-free grammars cannot be converted to equivalent unambiguous context-free grammars.

References

1. ^1 {{cite book |title=Automata and Computability|last=Kozen |first=Dexter|year=1997 |publisher=Springer-Verlag|location=New York|isbn=3-540-78105-6}}
2. ^{{cite web|url=http://www8.cs.umu.se/kurser/TDBC92/VT06/final/3.pdf|title=Parikh's theorem|author=Håkan Lindqvist|publisher=Umeå Universitet}}
3. ^{{cite journal |last1=Parikh |first1=Rohit|authorlink=Rohit Jivanlal Parikh|year=1961 |title=Language Generating Devices|journal=Quartly Progress Report, Research Laboratory of Electronics, MIT}}
4. ^{{cite journal |last1=Parikh |first1=Rohit|authorlink=Rohit Jivanlal Parikh|year=1966 |title=On Context-Free Languages|journal=Journal of the Association for Computing Machinery|volume=13|issue=4|url=http://portal.acm.org/citation.cfm?id=321364&dl=}}
5. ^{{cite journal |last1=Ginsburg|first1=Seymour|last2=Spanier|first2=Edwin H.|year=1966 |title=Presburger formulas, and languages|journal=Pacific Journal of Mathematics|volume=16|issue=2|pages=285-296|url=https://projecteuclid.org/euclid.pjm/1102994974}}

1 : Formal languages
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/13 18:36:19