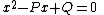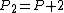- Recurrence relations
- Examples
- Explicit expressions Distinct roots Repeated root
- Properties Generating functions Sequences with the same discriminant Pell equations
- Other relations
- Specific names
- Applications
- See also
- Notes
- References
In mathematics, the Lucas sequences  and
and  are certain constant-recursive integer sequences that satisfy the recurrence relation
are certain constant-recursive integer sequences that satisfy the recurrence relation
where  and
and  are fixed integers. Any sequence satisfying this recurrence relation can be represented as a linear combination of the Lucas sequences
are fixed integers. Any sequence satisfying this recurrence relation can be represented as a linear combination of the Lucas sequences  and
and  .
.
More generally, Lucas sequences  and
and  represent sequences of polynomials in
represent sequences of polynomials in  and
and  with integer coefficients.
with integer coefficients.
Famous examples of Lucas sequences include the Fibonacci numbers, Mersenne numbers, Pell numbers, Lucas numbers, Jacobsthal numbers, and a superset of Fermat numbers. Lucas sequences are named after the French mathematician Édouard Lucas.
Recurrence relations
Given two integer parameters P and Q, the Lucas sequences of the first kind Un(P,Q) and of the second kind Vn(P,Q) are defined by the recurrence relations:
and
It is not hard to show that for  ,
,
Examples
Initial terms of Lucas sequences Un(P,Q) and Vn(P,Q) are given in the table:
Explicit expressions
The characteristic equation of the recurrence relation for Lucas sequences  and
and  is:
is:
It has the discriminant  and the roots:
and the roots:
Thus:
Note that the sequence  and the sequence
and the sequence  also satisfy the recurrence relation. However these might not be integer sequences.
also satisfy the recurrence relation. However these might not be integer sequences.
Distinct roots
When  , a and b are distinct and one quickly verifies that
, a and b are distinct and one quickly verifies that
.
It follows that the terms of Lucas sequences can be expressed in terms of a and b as follows
Repeated root
The case 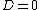 occurs exactly when
occurs exactly when  for some integer S so that
for some integer S so that 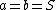 . In this case one easily finds that
. In this case one easily finds that
.
Properties
Generating functions
The ordinary generating functions are
Sequences with the same discriminant
If the Lucas sequences  and
and  have
have
discriminant 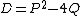 , then the sequences based on
, then the sequences based on  and
and  where
where
have the same discriminant:  .
.
Pell equations
When  , the Lucas sequences
, the Lucas sequences  and
and  satisfy certain Pell equations:
satisfy certain Pell equations:
Other relations
The terms of Lucas sequences satisfy relations that are generalizations of those between Fibonacci numbers 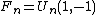 and Lucas numbers
and Lucas numbers 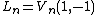 . For example:
. For example:
Among the consequences is that  is a multiple of
is a multiple of  , i.e., the sequence
, i.e., the sequence 
is a divisibility sequence. This implies, in particular, that  can be prime only when n is prime.
can be prime only when n is prime.
Another consequence is an analog of exponentiation by squaring that allows fast computation of  for large values of n.
for large values of n.
Moreover, if  , then
, then  is a strong divisibility sequence.
is a strong divisibility sequence.
Other divisibility properties are as follows:[1]
- If n / m is odd, then
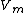 divides
divides  .
. - Let N be an integer relatively prime to 2Q. If the smallest positive integer r for which N divides
 exists, then the set of n for which N divides
exists, then the set of n for which N divides  is exactly the set of multiples of r.
is exactly the set of multiples of r. - If P and Q are even, then
 are always even except
are always even except 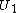 .
. - If P is even and Q is odd, then the parity of
 is the same as n and
is the same as n and  is always even.
is always even. - If P is odd and Q is even, then
 are always odd for
are always odd for 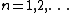 .
. - If P and Q are odd, then
 are even if and only if n is a multiple of 3.
are even if and only if n is a multiple of 3. - If p is an odd prime, then
 (see Legendre symbol).
(see Legendre symbol). - If p is an odd prime and divides P and Q, then p divides
 for every
for every  .
. - If p is an odd prime and divides P but not Q, then p divides
 if and only if n is even.
if and only if n is even. - If p is an odd prime and divides not P but Q, then p never divides
 for
for 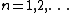 .
. - If p is an odd prime and divides not PQ but D, then p divides
 if and only if p divides n.
if and only if p divides n. - If p is an odd prime and does not divide PQD, then p divides
 , where
, where  .
.
The last fact generalizes Fermat's little theorem. These facts are used in the Lucas–Lehmer primality test.
The converse of the last fact does not hold, as the converse of Fermat's little theorem does not hold. There exists a composite n relatively prime to D and dividing  , where
, where  . Such a composite is called Lucas pseudoprime.
. Such a composite is called Lucas pseudoprime.
A prime factor of a term in a Lucas sequence that does not divide any earlier term in the sequence is called primitive.
Carmichael's theorem states that all but finitely many of the terms in a Lucas sequence have a primitive prime factor.[2] Indeed, Carmichael (1913) showed that if D is positive and n is not 1, 2 or 6, then  has a primitive prime factor. In the case D is negative, a deep result of Bilu, Hanrot, Voutier and Mignotte[3] shows that if n > 30, then
has a primitive prime factor. In the case D is negative, a deep result of Bilu, Hanrot, Voutier and Mignotte[3] shows that if n > 30, then  has a primitive prime factor and determines all cases
has a primitive prime factor and determines all cases  has no primitive prime factor.
has no primitive prime factor.
Specific names
The Lucas sequences for some values of P and Q have specific names:
{{math|Un(1,−1)}} : Fibonacci numbers
{{math|Vn(1,−1)}} : Lucas numbers
{{math|Un(2,−1)}} : Pell numbers
{{math|Vn(2,−1)}} : Pell-Lucas numbers (companion Pell numbers)
{{math|Un(1,−2)}} : Jacobsthal numbers
{{math|Vn(1,−2)}} : Jacobsthal-Lucas numbers
{{math|Un(3, 2)}} : Mersenne numbers 2n − 1
{{math|Vn(3, 2)}} : Numbers of the form 2n + 1, which include the Fermat numbers {{harv|Yabuta|2001}}.
{{math|Un(6, 1)}} : The square roots of the square triangular numbers.
{{math|Un(x,−1)}} : Fibonacci polynomials
{{math|Vn(x,−1)}} : Lucas polynomials
{{math|Un(2x, 1)}} : Chebyshev polynomials of second kind
{{math|Vn(2x, 1)}} : Chebyshev polynomials of first kind multiplied by 2
{{math|Un(x+1, x)}} : Repunits base x
{{math|Vn(x+1, x)}} : xn + 1
Some Lucas sequences have entries in the On-Line Encyclopedia of Integer Sequences:
 |  | 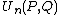 | 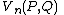 |
|---|---|---|---|
| −1 | 3 | A214733}} | |
| 1 | −1 | A000045}} | A000032}} |
| 1 | 1 | A128834}} | A087204}} |
| 1 | 2 | A107920}} | A002249}} |
| 2 | −1 | A000129}} | A002203}} |
| 2 | 1 | A001477}} | |
| 2 | 2 | A009545}} | A007395}} |
| 2 | 3 | A088137}} | |
| 2 | 4 | A088138}} | |
| 2 | 5 | A045873}} | |
| 3 | −5 | A015523}} | A072263}} |
| 3 | −4 | A015521}} | A201455}} |
| 3 | −3 | A030195}} | A172012}} |
| 3 | −2 | A007482}} | A206776}} |
| 3 | −1 | A006190}} | A006497}} |
| 3 | 1 | A001906}} | A005248}} |
| 3 | 2 | A000225}} | A000051}} |
| 3 | 5 | A190959}} | |
| 4 | −3 | A015530}} | A080042}} |
| 4 | −2 | A090017}} | |
| 4 | −1 | A001076}} | A014448}} |
| 4 | 1 | A001353}} | A003500}} |
| 4 | 2 | A007070}} | A056236}} |
| 4 | 3 | A003462}} | A034472}} |
| 4 | 4 | A001787}} | |
| 5 | −3 | A015536}} | |
| 5 | −2 | A015535}} | |
| 5 | −1 | A052918}} | A087130}} |
| 5 | 1 | A004254}} | A003501}} |
| 5 | 4 | A002450}} | A052539}} |
| 6 | 1 | A001109}} | A003499}} |
Applications
- Lucas sequences are used in probabilistic Lucas pseudoprime tests, which are part of the commonly used Baillie-PSW primality test.
- Lucas sequences are used in some primality proof methods, including the Lucas-Lehmer-Riesel test, and the N+1 and hybrid N-1/N+1 methods such as those in Brillhart-Lehmer-Selfridge 1975[4]
- LUC is a public-key cryptosystem based on Lucas sequences[5] that implements the analogs of ElGamal (LUCELG), Diffie-Hellman (LUCDIF), and RSA (LUCRSA). The encryption of the message in LUC is computed as a term of certain Lucas sequence, instead of using modular exponentiation as in RSA or Diffie-Hellman. However, a paper by Bleichenbacher et al.[6] shows that many of the supposed security advantages of LUC over cryptosystems based on modular exponentiation are either not present, or not as substantial as claimed.
See also
- Somer–Lucas pseudoprime
Notes
2. ^{{cite journal |last1=Yabuta |first1=M |title=A simple proof of Carmichael's theorem on primitive divisors |journal=Fibonacci Quarterly |date=2001 |volume=39 |pages=439–443 |url=http://www.fq.math.ca/Scanned/39-5/yabuta.pdf |accessdate=4 October 2018}}
3. ^{{cite journal | first1=Yuri | last1=Bilu | first2=Guillaume | last2=Hanrot | first3=Paul M. | last3=Voutier | first4=Maurice | last4=Mignotte | title=Existence of primitive divisors of Lucas and Lehmer numbers | journal = J. Reine Angew. Math. | year=2001 | volume=539 |pages= 75–122 | mr=1863855 | doi=10.1515/crll.2001.080}}
4. ^{{ cite journal|author=John Brillhart|author2=Derrick Henry Lehmer|author3=John Selfridge|title=New Primality Criteria and Factorizations of 2m ± 1|journal=Mathematics of Computation |volume=29|number=130|date=April 1975|pages=620–647|jstor=2005583|doi=10.1090/S0025-5718-1975-0384673-1}}
5. ^{{cite journal |author1=P. J. Smith |author2=M. J. J. Lennon |title=LUC: A new public key system |journal=Proceedings of the Ninth IFIP Int. Symp. on Computer Security |year=1993 |pages=103–117 |url=http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.32.1835}}
6. ^{{cite journal |author1=D. Bleichenbacher |author2=W. Bosma |author3=A. K. Lenstra |title=Some Remarks on Lucas-Based Cryptosystems |journal=Lecture Notes in Computer Science |volume=963 |year=1995 |pages=386–396 |doi=10.1007/3-540-44750-4_31 |url=http://www.math.ru.nl/~bosma/pubs/CRYPTO95.pdf}}
References
- {{citation
| last = Carmichael | first = R. D. | author-link = Robert Daniel Carmichael
| doi = 10.2307/1967797
| issue = 1/4
| journal = Annals of Mathematics
| pages = 30–70
| title = On the numerical factors of the arithmetic forms αn±βn
| volume = 15
| year = 1913
| jstor = 1967797 |ref=harv}}
- {{cite journal| first1=D. H. | last1=Lehmer
|title=An extended theory of Lucas' functions
|journal=Annals of Mathematics |year=1930
|volume=31 | number=3
|jstor=1968235 |pages=419–448 |bibcode=1930AnMat..31..419L | doi=10.2307/1968235
|ref=harv}}
- {{cite journal| first1=Morgan | last1=Ward
|title=Prime divisors of second order recurring sequences
|journal = Duke Math. J. | year=1954 | volume=21 | number=4
|pages=607–614 | mr=0064073 |doi=10.1215/S0012-7094-54-02163-8
|ref=harv}}
- {{cite journal|first1=Lawrence | last1=Somer
|title=The divisibility properties of primary Lucas Recurrences with respect to primes
|year=1980 | journal=Fibonacci Quarterly | pages=316 | volume=18 | url=http://www.fq.math.ca/Scanned/18-4/somer.pdf
|ref=harv}}
- {{cite journal|first1=J. C. | last1=Lagarias
|journal=Pac. J. Math. | title=The set of primes dividing Lucas Numbers has density 2/3
|year=1985 | volume=118 | number=2 | pages=449–461 | mr=789184 | doi=10.2140/pjm.1985.118.449
|ref=harv}}
- {{cite book | title=Prime Numbers and Computer Methods for Factorization | edition=2nd | author=Hans Riesel | authorlink=Hans Riesel | series=Progress in Mathematics | volume=126 | publisher=Birkhäuser | year=1994 | isbn=0-8176-3743-5 | pages=107–121 |ref=harv}}
- {{ cite journal|first1=Paulo | last1=Ribenboim | first2=Wayne L. |last2=McDaniel
|title=The square terms in Lucas Sequences | journal=J. Number Theory |year=1996 | volume=58 | number=1 | pages=104–123 | doi=10.1006/jnth.1996.0068
|ref=harv}}
- {{cite journal | first1=M. | last1=Joye | first2=J.-J. | last2=Quisquater | title=Efficient computation of full Lucas sequences | journal=Electronics Letters | year=1996 | volume=32 | number=6 | pages=537–538 | url=http://www.joye.site88.net/papers/JQ96lucas.pdf | doi=10.1049/el:19960359 | deadurl=yes | archiveurl=https://web.archive.org/web/20150202074230/http://www.joye.site88.net/papers/JQ96lucas.pdf | archivedate=2015-02-02 |ref=harv}}
- {{cite book |first= Paulo |last= Ribenboim |title=The New Book of Prime Number Records | publisher=Springer-Verlag, New York | edition=eBook | isbn=978-1-4612-0759-7 | DOI=10.1007/978-1-4612-0759-7 | year=1996|ref=harv}}
- {{cite book | first=Paulo | last=Ribenboim | authorlink=Paulo Ribenboim | year=2000 | title=My Numbers, My Friends: Popular Lectures on Number Theory | edition= | publisher=Springer-Verlag | location=New York | isbn=0-387-98911-0 | pages=1–50 |ref=harv}}
- {{cite journal | first1=Florian | last1=Luca
|title=Perfect Fibonacci and Lucas numbers | year=2000
|journal = Rend. Circ Matem. Palermo
|doi=10.1007/BF02904236 | volume=49 | number=2 | pages=313–318
|ref=harv}}
- {{cite journal
| last = Yabuta | first = M.
| journal = Fibonacci Quarterly
| pages = 439–443
| title = A simple proof of Carmichael's theorem on primitive divisors
| url = http://www.fq.math.ca/Scanned/39-5/yabuta.pdf
| volume = 39
| year = 2001
| ref=harv}}
- {{cite book
| title = Proofs that Really Count: The Art of Combinatorial Proof
| first1 = Arthur T. | last1 = Benjamin | author1-link = Arthur T. Benjamin
| first2 = Jennifer J. | last2 = Quinn | author2-link = Jennifer Quinn
| page = 35
| publisher = Mathematical Association of America
| series = Dolciani Mathematical Expositions
| volume = 27
| year = 2003
| isbn = 978-0-88385-333-7
| ref=harv}}
- [https://www.encyclopediaofmath.org/index.php/Lucas_sequence Lucas sequence] at Encyclopedia of Mathematics.
- {{MathWorld | urlname=LucasSequence | title=Lucas Sequence}}
- {{cite web| url = http://weidai.com/lucas.html|author=Wei Dai|title= Lucas Sequences in Cryptography}}
- Cocoon Crash
- Cocoon (film)
- Cocooning
- Cocoon (movie)
- Cocoon (Pokémon)
- Cocoons
- Cocoon (silk)
- Cocoon: The Return
- Cocopah
- Cocopah Tribe of Arizona
- Cocoparra National Park
- Coco Puffs
- Coco/R
- Coco River
- Cocorná
- Coco Robicheaux
- Cocoroc, Victoria
- Cocorosie
- CocoRosie
- Cocos
- Cocos Island
- Cocos Islands
- Cocos Islands/Communications
- Cocos Islands/Economy
- Cocos Islands/Geography