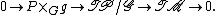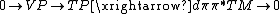“Atiyah algebroid”的意思、由来-开放百科全书

词条

Atiyah algebroid

释义

Direct construction
Lie groupoid viewpoint
References

{{Redirect|Atiyah sequence|the spectral sequence of Atiyah and Hirzebruch|Atiyah–Hirzebruch spectral sequence}}

In mathematics, the Atiyah algebroid, or Atiyah sequence, of a principal G-bundle P over a manifold M, where G is a Lie group, is the Lie algebroid of the gauge groupoid of P. Explicitly, it is given by the following short exact sequence of vector bundles over M:

It is named after Michael Atiyah, who introduced the construction to study the existence theory of complex analytic connections, and it has applications in gauge theory and mechanics.

Direct construction

For any fiber bundle P over a manifold M, with projection π: P→M, the differential dπ of π defines a short exact sequence

of vector bundles over P, where the vertical bundle VP is the kernel of the differential projection.

If P is a principal G-bundle, then the group G acts on the vector bundles in this sequence. The vertical bundle is isomorphic to the trivial g bundle over P, where g is the Lie algebra of G, and the quotient by the diagonal G action is the associated bundle P ×_G g. The quotient by G of this exact sequence thus yields the Atiyah sequence of vector bundles over M.

Lie groupoid viewpoint

Any principal G-bundle P→M has a gauge groupoid, whose objects are points of M, and whose morphisms are elements of the quotient of P×P by the diagonal action of G, with source and target given by the two projections of M. The Lie algebroid of this Lie groupoid is the Atiyah algebroid.

The space of sections of the Atiyah algebroid over M is the Lie algebra of G-invariant vector fields on P under Lie bracket, which is an extension of the Lie algebra of vector fields on M by the G-invariant vertical vector fields. In an algebraic or analytic context, it is more convenient to view the Atiyah algebroid as an exact sequence of sheaves of local sections of vector bundles.

References

{{citation|author=Michael F. Atiyah|title= Complex analytic connections in fibre bundles|journal=Trans. Amer. Math. Soc.|volume= 85|year=1957|pages=181–207|doi=10.1090/s0002-9947-1957-0086359-5}}.
{{citation|title=Geometric structures encoded in the lie structure of an Atiyah algebroid|author=Janusz Grabowski|author2=Alexei Kotov|author3=Norbert Poncin|last-author-amp=yes|journal=Transformation Groups|volume=16|year=2011|pages=137–160|doi=10.1007/s00031-011-9126-9|arxiv=0905.1226}}, available as [https://arxiv.org/abs/0905.1226 arXiv:0905.1226].
{{citation|title=Lie groupoids and Lie algebroids in differential geometry|volume=124|series=London Mathematical Society lecture notes|publisher=CUP|author= Kirill Mackenzie|year=1987|isbn=978-0-521-34882-9}}.
{{citation|title=General theory of lie groupoids and lie algebroids|volume=213|series=London Mathematical Society lecture notes|publisher=CUP|author= Kirill Mackenzie|year=2005|isbn=978-0-521-49928-6}}.
{{citation|title=A Lie algebroid framework for non-holonomic systems|author=Tom Mestdag|author2=Bavo Langerock|last-author-amp=yes|doi=10.1088/0305-4470/38/5/011|journal=J. Phys. A: Math. Gen.|volume= 38|year=2005|pages=1097–1111|arxiv=math/0410460|bibcode=2005JPhA...38.1097M}}.

1 : Lie algebras

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。