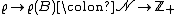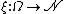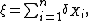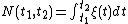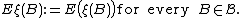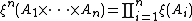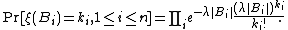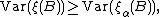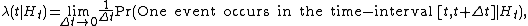- General point process theory Definition Representation Expectation measure Laplace functional Moment measure Stationarity
- Examples of point processes Poisson point process Cox point process Determinantal point processes Hawkes (self-exciting) processes Geometric processes
- Point processes on the real half-line Intensity of a point process
- Related functions Papangelou intensity function Likelihood function
- Point processes in spatial statistics
- See also
- Notes
- References
In statistics and probability theory, a point process or point field is a collection of mathematical points randomly located on some underlying mathematical space such as the real line, the Cartesian plane, or more abstract spaces. Point processes can be used as mathematical models of phenomena or objects representable as points in some type of space.
There are different mathematical interpretations of a point process, such as a random counting measure or a random set.[1][2] Some authors regard a point process and stochastic process as two different objects such that a point process is a random object that arises from or is associated with a stochastic process,[3][4] though it has been remarked that the difference between point processes and stochastic processes is not clear.[4] Others consider a point process as a stochastic process, where the process is indexed by sets of the underlying space{{efn|In the context of point processes, the term "state space" can mean the space on which the point process is defined such as the real line,[5][6] which corresponds to the index set in stochastic process terminology.}} on which it is defined, such as the real line or  -dimensional Euclidean space.[7][8] Other stochastic processes such as renewal and counting processes are studied in the theory of point processes.[9][10] Sometimes the term "point process" is not preferred, as historically the word "process" denoted an evolution of some system in time, so point process is also called a random point field.[11]
-dimensional Euclidean space.[7][8] Other stochastic processes such as renewal and counting processes are studied in the theory of point processes.[9][10] Sometimes the term "point process" is not preferred, as historically the word "process" denoted an evolution of some system in time, so point process is also called a random point field.[11]
Point processes are well studied objects in probability theory[12][13] and the subject of powerful tools in statistics for modeling and analyzing spatial data,[14][15] which is of interest in such diverse disciplines as forestry, plant ecology, epidemiology, geography, seismology, materials science, astronomy, telecommunications, computational neuroscience,[16] economics[17] and others.
Point processes on the real line form an important special case that is particularly amenable to study,[18] because the points are ordered in a natural way, and the whole point process can be described completely by the (random) intervals between the points. These point processes are frequently used as models for random events in time, such as the arrival of customers in a queue (queueing theory), of impulses in a neuron (computational neuroscience), particles in a Geiger counter, location of radio stations in a telecommunication network[19] or of searches on the world-wide web.
General point process theory
In mathematics, a point process is a random element whose values are "point patterns" on a set S. While in the exact mathematical definition a point pattern is specified as a locally finite counting measure, it is sufficient for more applied purposes to think of a point pattern as a countable subset of S that has no limit points.{{clarify|date=October 2011}}
Definition
Let S be a locally compact second countable Hausdorff space equipped with its Borel σ-algebra B(S). Write  for the set of locally finite counting measures on S and
for the set of locally finite counting measures on S and  for the smallest σ-algebra on
for the smallest σ-algebra on  that renders all the point counts
that renders all the point counts
measurable for all relatively compact sets B in B(S).
A point process on S is a measurable map
from a probability space  to the measurable space
to the measurable space 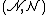 .
.
By this definition, a point process is a special case of a random measure.
The most common example for the state space S is the Euclidean space Rn or a subset thereof, where a particularly interesting special case is given by the real half-line [0,∞). However, point processes are not limited to these examples and may among other things also be used if the points are themselves compact subsets of Rn, in which case ξ is usually referred to as a particle process.
It has been noted{{Citation needed|date=June 2007}} that the term point process is not a very good one if S is not a subset of the real line, as it might suggest that ξ is a stochastic process. However, the term is well established and uncontested even in the general case.
Representation
Every instance (or event) of a point process ξ can be represented as
where  denotes the Dirac measure, n is an integer-valued random variable and
denotes the Dirac measure, n is an integer-valued random variable and  are random elements of S. If
are random elements of S. If  's are almost surely distinct (or equivalently, almost surely
's are almost surely distinct (or equivalently, almost surely 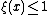 for all
for all 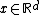 ), then the point process is known as simple.
), then the point process is known as simple.
Another different but useful representation of an event (an event in the event space, i.e. a series of points) is the counting notation, where each instance is represented as an 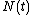 function, a continuous function which takes integer values:
function, a continuous function which takes integer values: 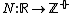 :
:
which is the number of events in the observation interval  . It is sometimes shown as
. It is sometimes shown as  and
and 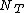 or
or  means
means 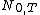 .
.
Expectation measure
{{main|Intensity measure}}The expectation measure Eξ (also known as mean measure) of a point process ξ is a measure on S that assigns to every Borel subset B of S the expected number of points of ξ in B. That is,
Laplace functional
The Laplace functional 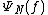 of a point process N is a
of a point process N is a
map from the set of all positive valued functions f on the state space of N, to  defined as follows:
defined as follows:
They play a similar role as the characteristic functions for random variable. One important theorem says that: two point processes have the same law if their Laplace functionals are equal.
Moment measure
{{Main|Moment measure}}The  th power of a point process,
th power of a point process, 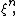 is defined on the product space
is defined on the product space  as follows :
as follows :
By monotone class theorem, this uniquely defines the product measure on  The expectation
The expectation 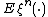 is called
is called
the  th moment measure. The first moment measure is the mean measure.
th moment measure. The first moment measure is the mean measure.
Let 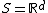 . The joint intensities of a point process
. The joint intensities of a point process  w.r.t. the Lebesgue measure are functions
w.r.t. the Lebesgue measure are functions 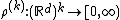 such that for any disjoint bounded Borel subsets
such that for any disjoint bounded Borel subsets 
Joint intensities do not always exist for point processes. Given that moments of a random variable determine the random variable in many cases, a similar result is to be expected for joint intensities. Indeed, this has been shown in many cases.[13]
Stationarity
A point process 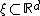 is said to be stationary if
is said to be stationary if 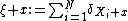 has the same distribution as
has the same distribution as  for all
for all 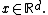 For a stationary point process, the mean measure
For a stationary point process, the mean measure 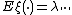 for some constant
for some constant  and where
and where  stands for the Lebesgue measure. This
stands for the Lebesgue measure. This  is called the intensity of the point process. A stationary point process on
is called the intensity of the point process. A stationary point process on  has almost surely either 0 or an infinite number of points in total. For more on stationary point processes and random measure, refer to Chapter 12 of Daley & Vere-Jones.[13] It is to be noted that stationarity has been defined and studied for point processes in more general spaces than
has almost surely either 0 or an infinite number of points in total. For more on stationary point processes and random measure, refer to Chapter 12 of Daley & Vere-Jones.[13] It is to be noted that stationarity has been defined and studied for point processes in more general spaces than  .
.
Examples of point processes
We shall see some examples of point processes in 
Poisson point process
{{Main|Poisson point process}}The simplest and most ubiquitous example of a point process is the Poisson point process, which is a spatial generalisation of the Poisson process. A Poisson (counting) process on the line can be characterised by two properties : the number of points (or events) in disjoint intervals are independent and have a Poisson distribution. A Poisson point process can also be defined using these two properties. Namely, we say that a point process  is a Poisson point process if the following two conditions hold
is a Poisson point process if the following two conditions hold
1)  are independent for disjoint subsets
are independent for disjoint subsets

2) For any bounded subset  ,
, 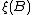 has a Poisson distribution with parameter
has a Poisson distribution with parameter  where
where
 denotes the Lebesgue measure.
denotes the Lebesgue measure.
The two conditions can be combined together and written as follows : For any disjoint bounded subsets 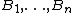 and non-negative integers
and non-negative integers 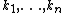 we have that
we have that
The constant  is called the intensity of the Poisson point process. Note that the Poisson point process is characterised by the single parameter
is called the intensity of the Poisson point process. Note that the Poisson point process is characterised by the single parameter 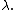 It is a simple, stationary point process.
It is a simple, stationary point process.
To be more specific one calls the above point process, a homogeneous Poisson point process. An inhomogeneous Poisson process is defined as above but by replacing  with
with  where
where  is a non-negative function on
is a non-negative function on 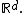
Cox point process
A Cox process (named after Sir David Cox) is a generalisation of the Poisson point process, in that we use random measures in place of  . More formally, let
. More formally, let  be a random measure. A Cox point process driven by the random measure
be a random measure. A Cox point process driven by the random measure  is the point process
is the point process  with the following two properties :
with the following two properties :
- Given
 ,
, 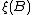 is Poisson distributed with parameter
is Poisson distributed with parameter 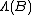 for any bounded subset
for any bounded subset 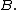
- For any finite collection of disjoint subsets
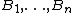 and conditioned on
and conditioned on 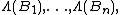 we have that
we have that  are independent.
are independent.
It is easy to see that Poisson point process (homogeneous and inhomogeneous) follow as special cases of Cox point processes. The mean measure of a Cox point process is 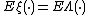 and thus in the special case of a Poisson point process, it is
and thus in the special case of a Poisson point process, it is 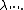
For a Cox point process,  is called the intensity measure. Further, if
is called the intensity measure. Further, if  has a (random) density (Radon–Nikodym derivative)
has a (random) density (Radon–Nikodym derivative)  i.e.,
i.e.,
then  is called the intensity field of the Cox point process. Stationarity of the intensity measures or intensity fields imply the stationarity of the corresponding Cox point processes.
is called the intensity field of the Cox point process. Stationarity of the intensity measures or intensity fields imply the stationarity of the corresponding Cox point processes.
There have been many specific classes of Cox point processes that have been studied in detail such as:
- Log Gaussian Cox point processes:[20]
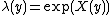 for a Gaussian random field
for a Gaussian random field 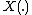
- Shot noise Cox point processes:,[21]
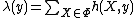 for a Poisson point process
for a Poisson point process  and kernel
and kernel 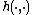
- Generalised shot noise Cox point processes:[22]
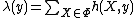 for a point process
for a point process  and kernel
and kernel 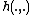
- Lévy based Cox point processes:[23]
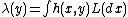 for a Lévy basis
for a Lévy basis 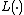 and kernel
and kernel 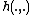 , and
, and - Permanental Cox point processes:[24]
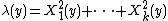 for k independent Gaussian random fields
for k independent Gaussian random fields  's
's - Sigmoidal Gaussian Cox point processes:[25]
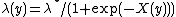 for a Gaussian random field
for a Gaussian random field  and random
and random 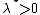
By Jensen's inequality, one can verify that Cox point processes satisfy the following inequality: for all bounded Borel subsets  ,
,
where 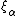 stands for a Poisson point process with intensity measure
stands for a Poisson point process with intensity measure  Thus points are distributed with greater variability in a Cox point process compared to a Poisson point process. This is sometimes called clustering or attractive property of the Cox point process.
Thus points are distributed with greater variability in a Cox point process compared to a Poisson point process. This is sometimes called clustering or attractive property of the Cox point process.
Determinantal point processes
An important class of point processes, with applications to physics, random matrix theory, and combinatorics, is that of determinantal point processes.[26]
Hawkes (self-exciting) processes
A Hawkes process 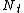 , also known as a self-exciting counting process, is a simple point process whose conditional intensity can be expressed as
, also known as a self-exciting counting process, is a simple point process whose conditional intensity can be expressed as
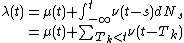
where 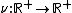 is a kernel function which expresses the positive influence of past events
is a kernel function which expresses the positive influence of past events  on the current value of the intensity process
on the current value of the intensity process  ,
, 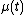 is a possibly non-stationary function representing the expected, predictable, or deterministic part of the intensity, and
is a possibly non-stationary function representing the expected, predictable, or deterministic part of the intensity, and 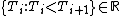 is the time of occurrence of the i-th event of the process.{{citation needed|date=November 2017}}
is the time of occurrence of the i-th event of the process.{{citation needed|date=November 2017}}
Geometric processes
Given a sequence of non-negative random variables :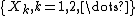 , if they are independent and the cdf of
, if they are independent and the cdf of  is given by
is given by 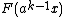 for
for  , where
, where  is a positive constant, then
is a positive constant, then  is called a geometric process (GP) [27].
is called a geometric process (GP) [27].
The geometric process has several extensions, including the α- series process[28] and the doubly geometric process [29].
Point processes on the real half-line
Historically the first point processes that were studied had the real half line R+ = [0,∞) as their state space, which in this context is usually interpreted as time. These studies were motivated by the wish to model telecommunication systems,[30] in which the points represented events in time, such as calls to a telephone exchange.
Point processes on R+ are typically described by giving the sequence of their (random) inter-event times (T1, T2, ...), from which the actual sequence (X1, X2, ...) of event times can be obtained as
If the inter-event times are independent and identically distributed, the point process obtained is called a renewal process.
Intensity of a point process
The intensity λ(t | Ht) of a point process on the real half-line with respect to a filtration Ht is defined as
Ht can denote the history of event-point times preceding time t but can also correspond to other filtrations (for example in the case of a Cox process).
In the 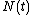 -notation, this can be written in a more compact form:
-notation, this can be written in a more compact form:
 .
.
The compensator of a point process, also known as the dual-predictable projection, is the integrated conditional intensity function defined by
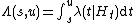
Related functions
Papangelou intensity function
The Papangelou intensity function of a point process  in the
in the  -dimensional Euclidean space
-dimensional Euclidean space 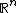
is defined as
where 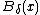 is the ball centered at
is the ball centered at  of a radius
of a radius  , and
, and  denotes the information of the point process
denotes the information of the point process 
outside  .
.
Likelihood function
The logarithmic likelihood of a parameterized simple point process conditional upon some observed data is written as
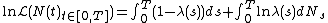 [31]
[31]Point processes in spatial statistics
The analysis of point pattern data in a compact subset S of Rn is a major object of study within spatial statistics. Such data appear in a broad range of disciplines,[32] amongst which are
- forestry and plant ecology (positions of trees or plants in general)
- epidemiology (home locations of infected patients)
- zoology (burrows or nests of animals)
- geography (positions of human settlements, towns or cities)
- seismology (epicenters of earthquakes)
- materials science (positions of defects in industrial materials)
- astronomy (locations of stars or galaxies)
- computational neuroscience (spikes of neurons).
The need to use point processes to model these kinds of data lies in their inherent spatial structure. Accordingly, a first question of interest is often whether the given data exhibit complete spatial randomness (i.e. are a realization of a spatial Poisson process) as opposed to exhibiting either spatial aggregation or spatial inhibition.
In contrast, many datasets considered in classical multivariate statistics consist of independently generated datapoints that may be governed by one or several covariates (typically non-spatial).
Apart from the applications in spatial statistics, point processes are one of the fundamental objects in stochastic geometry. Research has also focussed extensively on various models built on point processes such as Voronoi Tessellations, Random geometric graphs, Boolean model etc.
See also
- Empirical measure
- Random measure
- Point process notation
- Point process operation
- Poisson process
- Renewal theory
- Invariant measure
- Transfer operator
- Koopman operator
- Shift operator
Notes
{{notelist}}References
2. ^{{cite book|author=Martin Haenggi|title=Stochastic Geometry for Wireless Networks|url=https://books.google.com/books?id=CLtDhblwWEgC|year=2013|publisher=Cambridge University Press|isbn=978-1-107-01469-5|page=10}}
3. ^{{cite book|author1=D.J. Daley|author2=D. Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods|url=https://books.google.com/books?id=6Sv4BwAAQBAJ|date=10 April 2006|publisher=Springer Science & Business Media|isbn=978-0-387-21564-8|page=194}}
4. ^1 {{cite book|author1=D.R. Cox|author2=Valerie Isham|title=Point Processes|url=https://books.google.com/books?id=KWF2xY6s3PoC|date=17 July 1980|publisher=CRC Press|isbn=978-0-412-21910-8|page=3}}
5. ^{{cite book|author=J. F. C. Kingman|title=Poisson Processes|url=https://books.google.com/books?id=VEiM-OtwDHkC|date=17 December 1992|publisher=Clarendon Press|isbn=978-0-19-159124-2|page=8}}
6. ^{{cite book|author1=Jesper Moller|author2=Rasmus Plenge Waagepetersen|title=Statistical Inference and Simulation for Spatial Point Processes|url=https://books.google.com/books?id=dBNOHvElXZ4C|date=25 September 2003|publisher=CRC Press|isbn=978-0-203-49693-0|page=7}}
7. ^{{cite book|author1=Samuel Karlin|author2=Howard E. Taylor|title=A First Course in Stochastic Processes|url=https://books.google.com/books?id=dSDxjX9nmmMC|date=2 December 2012|publisher=Academic Press|isbn=978-0-08-057041-9|page=31}}
8. ^{{cite book|author=Volker Schmidt|title=Stochastic Geometry, Spatial Statistics and Random Fields: Models and Algorithms|url=https://books.google.com/books?id=brsUBQAAQBAJ&pg=PR5|date=24 October 2014|publisher=Springer|isbn=978-3-319-10064-7|page=99}}
9. ^{{cite book|author1=D.J. Daley|author2=D. Vere-Jones|title=An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods|url=https://books.google.com/books?id=6Sv4BwAAQBAJ|date=10 April 2006|publisher=Springer Science & Business Media|isbn=978-0-387-21564-8}}
10. ^{{cite book|author1=D.R. Cox|author2=Valerie Isham|title=Point Processes|url=https://books.google.com/books?id=KWF2xY6s3PoC|date=17 July 1980|publisher=CRC Press|isbn=978-0-412-21910-8}}
11. ^{{cite book|author1=Sung Nok Chiu|author2=Dietrich Stoyan|author3=Wilfrid S. Kendall|author4=Joseph Mecke|title=Stochastic Geometry and Its Applications|url=https://books.google.com/books?id=825NfM6Nc-EC|date=27 June 2013|publisher=John Wiley & Sons|isbn=978-1-118-65825-3|page=109}}
12. ^Kallenberg, O. (1986). Random Measures, 4th edition. Academic Press, New York, London; Akademie-Verlag, Berlin. {{isbn|0-12-394960-2}}, {{MR|854102}}.
13. ^1 2 Daley, D.J, Vere-Jones, D. (1988). An Introduction to the Theory of Point Processes. Springer, New York. {{isbn|0-387-96666-8}}, {{MR|950166}}.
14. ^Diggle, P. (2003). Statistical Analysis of Spatial Point Patterns, 2nd edition. Arnold, London. {{isbn|0-340-74070-1}}.
15. ^Baddeley, A. (2006). Spatial point processes and their applications.In A. Baddeley, I. Bárány, R. Schneider, and W. Weil, editors, Stochastic Geometry: Lectures given at the C.I.M.E. Summer School held in Martina Franca, Italy, September 13–18, 2004, Lecture Notes in Mathematics 1892, Springer. {{isbn|3-540-38174-0}}, pp. 1–75
16. ^{{cite journal | author = Brown E. N., Kass R. E., Mitra P. P. | year = 2004 | title = Multiple neural spike train data analysis: state-of-the-art and future challenges | url = | journal = Nature Neuroscience | volume = 7 | issue = 5| pages = 456–461 | doi = 10.1038/nn1228 | pmid = 15114358 }}
17. ^{{cite journal | author = Engle Robert F., Lunde Asger | year = 2003 | title = Trades and Quotes: A Bivariate Point Process | url = | journal = Journal of Financial Econometrics | volume = 1 | issue = 2| pages = 159–188 | doi=10.1093/jjfinec/nbg011}}
18. ^Last, G., Brandt, A. (1995).Marked point processes on the real line: The dynamic approach. Probability and its Applications. Springer, New York. {{isbn|0-387-94547-4}}, {{MR|1353912}}
19. ^{{cite journal | author = Gilbert E.N. | authorlink = Edgar N. Gilbert | year = 1961 | title = Random plane networks | url = | journal = Journal of the Society for Industrial and Applied Mathematics | volume = 9 | issue = 4 | pages = 533–543 | doi = 10.1137/0109045 }}
20. ^{{Cite journal | last1 = Moller | first1 = J. | last2 = Syversveen | first2 = A. R. | last3 = Waagepetersen | first3 = R. P. | doi = 10.1111/1467-9469.00115 | title = Log Gaussian Cox Processes | journal = Scandinavian Journal of Statistics | volume = 25 | issue = 3 | pages = 451 | year = 1998 | pmid = | pmc = | citeseerx = 10.1.1.71.6732 }}
21. ^Moller, J. (2003) Shot noise Cox processes, Adv. Appl. Prob., 35.{{Page needed|date=October 2011}}
22. ^Moller, J. and Torrisi, G.L. (2005) "Generalised Shot noise Cox processes", Adv. Appl. Prob., 37.
23. ^Hellmund, G., Prokesova, M. and Vedel Jensen, E.B. (2008)"Lévy-based Cox point processes", Adv. Appl. Prob., 40. {{Page needed|date=October 2011}}
24. ^Mccullagh,P. and Moller, J. (2006) "The permanental processes", Adv. Appl. Prob., 38.{{Page needed|date=June 2011}}
25. ^Adams, R. P., Murray, I. MacKay, D. J. C. (2009) "Tractable inference in Poisson processes with Gaussian process intensities", Proceedings of the 26th International Conference on Machine Learning {{doi|10.1145/1553374.1553376}}
26. ^Hough, J. B., Krishnapur, M., Peres, Y., and Virág, B., Zeros of Gaussian analytic functions and determinantal point processes. University Lecture Series, 51. American Mathematical Society, Providence, RI, 2009.
27. ^{{Cite journal |doi = 10.1007/BF02007241|title = Geometric processes and replacement problem|journal = Acta Mathematicae Applicatae Sinica|volume = 4|issue = 4|pages = 366–377|year = 1988|last1 = Lin|first1 = Ye (Lam Yeh)}}
28. ^{{Cite journal |doi = 10.1002/nav.20099|title = Properties of the geometric and related processes|journal = Naval Research Logistics|volume = 52|issue = 7|pages = 607–616|year = 2005|last1 = Braun|first1 = W. John|last2 = Li|first2 = Wei|last3 = Zhao|first3 = Yiqiang Q.|citeseerx = 10.1.1.113.9550}}
29. ^{{Cite journal |doi = 10.1057/s41274-017-0217-4|title = Doubly geometric processes and applications|journal = Journal of the Operational Research Society|volume = 69|pages = 66–77|year = 2018|last1 = Wu|first1 = Shaomin}}
30. ^Palm, C. (1943). Intensitätsschwankungen im Fernsprechverkehr (German).Ericsson Technics no. 44, (1943). {{MR|11402}}
31. ^{{Cite journal|last=Rubin|first=I.|date=Sep 1972|title=Regular point processes and their detection|url=|journal=IEEE Transactions on Information Theory|volume=18|issue=5|pages=547–557|doi=10.1109/tit.1972.1054897}}
32. ^Baddeley, A., Gregori, P., Mateu, J., Stoica, R., and Stoyan, D., editors (2006). Case Studies in Spatial Point Pattern Modelling, Lecture Notes in Statistics No. 185. Springer, New York.{{isbn|0-387-28311-0}}.
- Gonner (video game)
- Gonnet, Charles
- Gonneville (disambiguation)
- Gonneville-le-Theil
- Gonnie McClung Siegel
- Gonnie Rietveld
- Gonnie Siegel
- Gonno-Condylon
- Gonnocondylum
- Gonnocondylus
- Gon no Kami
- Gonnos
- Gonnus
- Gono Adalat
- Gonobahini (Mukti Bahini)
- Gono Bhaban
- Gonobhaban
- Gonobitz
- Gonobombyx angulata
- Gonocarpus chinensis
- Gonocarpus micranthus
- Gonocarpus montanus
- Gonocephalus bellii
- Gonocephalus doriae
- Gonocephalus robinsonii