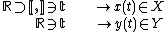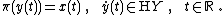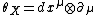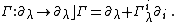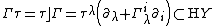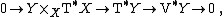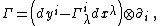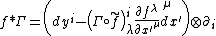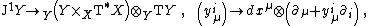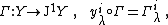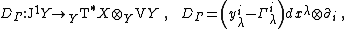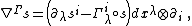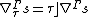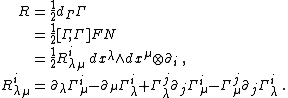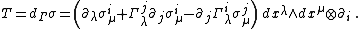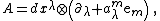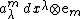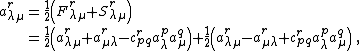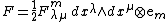- Formal definition Connection as a horizontal splitting Connection as a tangent-valued form Connection as a vertical-valued form Connection as a jet bundle section
- Curvature and torsion
- Bundle of principal connections
- See also
- Notes
- References
In differential geometry, a fibered manifold is surjective submersion of smooth manifolds {{math|Y → X}}. Locally trivial fibered manifolds are fiber bundles. Therefore, a notion of connection on fibered manifolds provides a general framework of a connection on fiber bundles.
Formal definition
Let {{math| π : Y → X}} be a fibered manifold. A generalized connection on {{mvar|Y}} is a section {{math|Γ : Y → J1Y}}, where {{math|J1Y}} is the jet manifold of {{mvar|Y}}.[1]
Connection as a horizontal splitting
With the above manifold {{mvar|π}} there is the following canonical short exact sequence of vector bundles over {{mvar|Y}}:
{{NumBlk|:|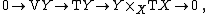 |{{EquationRef|1}}}}
|{{EquationRef|1}}}}where {{math|TY}} and {{math|TX}} are the tangent bundles of {{mvar|Y}}, respectively, {{math|VY}} is the vertical tangent bundle of {{mvar|Y}}, and {{math|Y ×X TX}} is the pullback bundle of {{math|TX}} onto {{mvar|Y}}.
A connection on a fibered manifold {{math|Y → X}} is defined as a linear bundle morphism
{{NumBlk|:|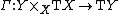 |{{EquationRef|2}}}}
|{{EquationRef|2}}}}over {{mvar|Y}} which splits the exact sequence {{EquationRef|1}}. A connection always exists.
Sometimes, this connection {{math|Γ}} is called the Ehresmann connection because it yields the horizontal distribution
of {{math|TY}} and its horizontal decomposition {{math|TY {{=}} VY ⊕ HY}}.
At the same time, by an Ehresmann connection also is meant the following construction. Any connection {{math|Γ}} on a fibered manifold {{math|Y → X}} yields a horizontal lift {{math|Γ ∘ τ}} of a vector field {{mvar|τ}} on {{mvar|X}} onto {{mvar|Y}}, but need not defines the similar lift of a path in {{mvar|X}} into {{mvar|Y}}. Let
be two smooth paths in {{mvar|X}} and {{mvar|Y}}, respectively. Then {{math|t → y(t)}} is called the horizontal lift of {{math|x(t)}} if
A connection {{math|Γ}} is said to be the Ehresmann connection if, for each path {{math|x([0,1])}} in {{mvar|X}}, there exists its horizontal lift through any point {{math|y ∈ π−1(x([0,1]))}}. A fibered manifold is a fiber bundle if and only if it admits such an Ehresmann connection.
Connection as a tangent-valued form
Given a fibered manifold {{math|Y → X}}, let it be endowed with an atlas of fibered coordinates {{math|(xμ, yi)}}, and let {{math|Γ}} be a connection on {{math|Y → X}}. It yields uniquely the horizontal tangent-valued one-form
{{NumBlk|:|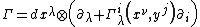 |{{EquationRef|3}}}}
|{{EquationRef|3}}}}on {{mvar|Y}} which projects onto the canonical tangent-valued form (tautological one-form or solder form)
on {{mvar|X}}, and vice versa. With this form, the horizontal splitting {{EquationNote|2}} reads
In particular, the connection {{math|Γ}} in {{EquationNote|3}} yields the horizontal lift of any vector field {{math|τ {{=}} τμ ∂μ}} on {{mvar|X}} to a projectable vector field
on {{mvar|Y}}.
Connection as a vertical-valued form
The horizontal splitting {{EquationNote|2}} of the exact sequence {{EquationNote|1}} defines the corresponding splitting of the dual exact sequence
where {{math|T*Y}} and {{math|T*X}} are the cotangent bundles of {{mvar|Y}}, respectively, and {{math|V*Y → Y}} is the dual bundle to {{math|VY → Y}}, called the vertical cotangent bundle. This splitting is given by the vertical-valued form
which also represents a connection on a fibered manifold.
Treating a connection as a vertical-valued form, one comes to the following important construction. Given a fibered manifold {{math|Y → X}}, let {{math|f : X′ → X}} be a morphism and {{math|f ∗ Y → X′}} the pullback bundle of {{mvar|Y}} by {{mvar|f}}. Then any connection {{math|Γ}} {{EquationNote|3}} on {{math|Y → X}} induces the pullback connection
on {{math|f ∗ Y → X′}}.
Connection as a jet bundle section
Let {{math|J1Y}} be the jet manifold of sections of a fibered manifold {{math|Y → X}}, with coordinates {{math|(xμ, yi, y{{su|p=i|b=μ}})}}. Due to the canonical imbedding
any connection {{math|Γ}} {{EquationNote|3}} on a fibered manifold {{math|Y → X}} is represented by a global section
of the jet bundle {{math|J1Y → Y}}, and vice versa. It is an affine bundle modelled on a vector bundle
{{NumBlk|:|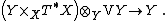 |{{EquationRef|4}}}}
|{{EquationRef|4}}}}There are the following corollaries of this fact.
{{ordered list|list_style_type=lower-roman|Connections on a fibered manifold {{math|Y → X}} make up an affine space modelled on the vector space of soldering forms{{NumBlk|:|
 |{{EquationRef|5}}}}
|{{EquationRef|5}}}}on {{math|Y → X}}, i.e., sections of the vector bundle {{EquationNote|4}}.
|Connection coefficients possess the coordinate transformation law
|Every connection {{math|Γ}} on a fibred manifold {{math|Y → X}} yields the first order differential operator
on {{mvar|Y}} called the covariant differential relative to the connection {{math|Γ}}. If {{math|s : X → Y}} is a section, its covariant differential
and the covariant derivative
along a vector field {{mvar|τ}} on {{mvar|X}} are defined.}}
Curvature and torsion
Given the connection {{math|Γ}} {{EquationNote|3}} on a fibered manifold {{math|Y → X}}, its curvature is defined as the Nijenhuis differential
This is a vertical-valued horizontal two-form on {{mvar|Y}}.
Given the connection {{math|Γ}} {{EquationNote|3}} and the soldering form {{mvar|σ}} {{EquationNote|5}}, a torsion of {{math|Γ}} with respect to {{mvar|σ}} is defined as
Bundle of principal connections
Let {{math|π : P → M}} be a principal bundle with a structure Lie group {{mvar|G}}. A principal connection on {{mvar|P}} usually is described by a Lie algebra-valued connection one-form on {{mvar|P}}. At the same time, a principal connection on {{mvar|P}} is a global section of the jet bundle {{math|J1P → P}} which is equivariant with respect to the canonical right action of {{mvar|G}} in {{mvar|P}}. Therefore, it is represented by a global section of the quotient bundle {{math|C {{=}} J1P/G → M}}, called the bundle of principal connections. It is an affine bundle modelled on the vector bundle {{math|VP/G → M}} whose typical fiber is the Lie algebra {{math|g}} of structure group {{mvar|G}}, and where {{mvar|G}} acts on by the adjoint representation. There is the canonical imbedding of {{mvar|C}} to the quotient bundle {{math|TP/G}} which also is called the bundle of principal connections.
Given a basis {{math|{em}|}} for a Lie algebra of {{mvar|G}}, the fiber bundle {{mvar|C}} is endowed with bundle coordinates {{math|(xμ, a{{su|p=m|b=μ}})}}, and its sections are represented by vector-valued one-forms
where
are the familiar local connection forms on {{mvar|M}}.
Let us note that the jet bundle {{math|J1C}} of {{mvar|C}} is a configuration space of Yang–Mills gauge theory. It admits the canonical decomposition
where
is called the strength form of a principal connection.
See also
- Connection (mathematics)
- Fibred manifold
- Ehresmann connection
- Connection (principal bundle)
Notes
References
- {{cite book|last1 = Kolář|first1=Ivan|last2=Michor|first2=Peter|last3=Slovák|first3=Jan|url=http://www.emis.de/monographs/KSM/kmsbookh.pdf|format=PDF|title=Natural operators in differential geometry|year = 1993|publisher = Springer-Verlag}}
- {{cite book|last1 = Krupka|first1=Demeter|last2=Janyška|first2=Josef|title=Lectures on differential invariants|year = 1990|publisher = Univerzita J. E. Purkyně v Brně|isbn=80-210-0165-8}}
- {{cite book|last1 = Saunders|first1=D.J.|title=The geometry of jet bundles|year = 1989|publisher = Cambridge University Press|isbn=0-521-36948-7}}
- {{cite book|last1=Mangiarotti|first1=L. |author2-link=Gennadi Sardanashvily|last2=Sardanashvily |first2=G. |title=Connections in Classical and Quantum Field Theory |publisher=World Scientific |date=2000 |ISBN= 981-02-2013-8}}
- {{cite book|authorlink=Gennadi Sardanashvily|last=Sardanashvily |first=G. |title=Advanced Differential Geometry for Theoreticians. Fiber bundles, jet manifolds and Lagrangian theory |publisher=Lambert Academic Publishing |date=2013 |ISBN= 978-3-659-37815-7 |arxiv=0908.1886|bibcode=2009arXiv0908.1886S }}
- Anne Arundel
- Anne Arundel Community College
- Anne Arundel County
- Anne Arundel County, Maryland
- Anne Arundel County, MD
- Anne Askew
- Anne Aubrey
- Anneau Hans-Reinhart
- Anne Ayres
- Anne Azéma
- Anne Bancroft
- Annebault
- Anne Baxter
- Anne Bayefsky
- Anne Beadell Highway
- Anne Beauchamp
- Anne Beauchamp, 15th Countess of Warwick
- Anne Beauchamp, 16th Countess of Warwick
- Anne Begg
- Anne Bishop
- Anne Blunt, 15th Baroness Wentworth
- Anne Bogart
- Anne Boleyn
- Anne Bonney
- Anne Bonny